The Detection, Extraction and Parameter Estimation of Extreme-Mass-Ratio Inspirals with Deep Learning

Qianyun Yun, Wen-Biao Han, Yi-Yang Guo, He Wang, Minghui Du
Last updated on Nov 13, 2024 Gravitational-wave Detection, Gravitational-wave Inference
PDF DOI
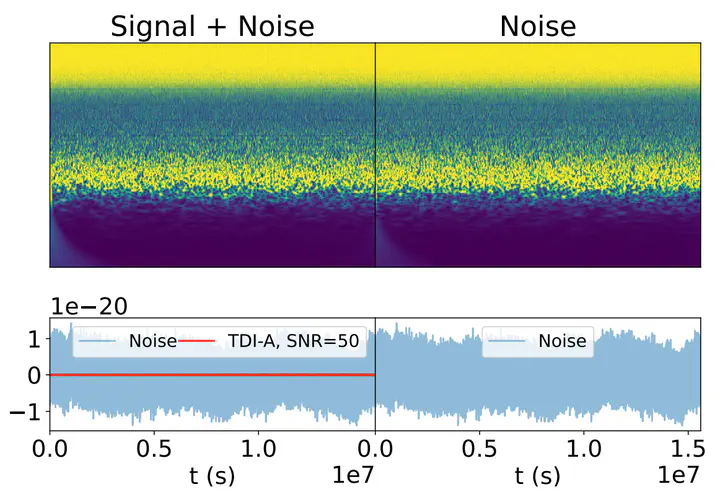Left: The CQT plot and the time series plot of signal and noise. Right: The CQT plot and the time series plot of pure noise.
Gravitational Waves EMRI AI CNN Detection inference
He Wang
He Wang
PostDoc

Knowledge increases by sharing but not by saving.