Advancing Space-Based Gravitational Wave Astronomy: Rapid Detection and Parameter Estimation Using Normalizing Flows

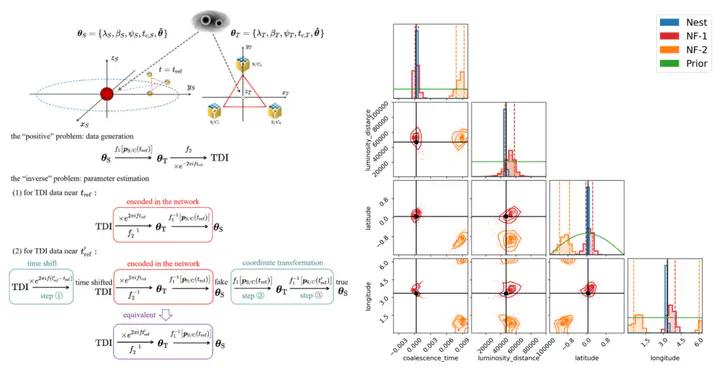Last updated on Feb 11, 2026 Gravitational-Wave Inference
PDF DOI
(Left) A schematic illustration depicting the generalization of our network during the inference stage. (Right) Extrinsic parameter posterior corner plot of injected signal in confusion noise with GBs.

Highlights

  • Space-Based Detection Focus: First application of normalizing flows specifically addressing unique challenges of Taiji space-based gravitational wave detector.

  • Confusion Noise Handling: Successfully performs parameter estimation in presence of galactic binary confusion noise, a critical challenge for space-based missions.

  • Time-Dependent Response: Innovative transformation mapping to overcome Taiji’s year-period time-dependent detector response function.

  • Multimodality Discovery: Reveals additional multimodal structures in arrival time parameter arising from orbital motion of space-based detectors.

  • Orders of Magnitude Speedup: Achieves rapid inference several orders faster than traditional nested sampling while maintaining high accuracy.

  • Rapid Detection Framework: Paves way for low-latency alert systems and real-time parameter estimation for massive black hole binary mergers.

Key Contributions

1. Space-Based Gravitational Wave Detection Challenges

Taiji Mission Overview

Taiji is China’s planned space-based gravitational wave detector:

  • Configuration: Three spacecraft in heliocentric orbit, forming triangular constellation
  • Arm Length: ~3 million kilometers (1000x longer than LIGO)
  • Frequency Band: millihertz range (0.1 mHz - 1 Hz)
  • Primary Targets: Massive black hole binaries, extreme mass ratio inspirals, galactic binaries
  • Launch Timeline: 2030s

Unique Challenges vs. Ground-Based

Time-Varying Detector Response

  • Spacecraft constellation orbits the Sun with 1-year period
  • Detector orientation changes continuously
  • Amplitude and phase modulation in observed signals
  • Response function depends on time and sky location
  • Traditional analysis assumes stationary detector

Galactic Confusion Noise

  • Tens of millions of unresolved white dwarf binaries in Milky Way
  • Creates stochastic foreground dominating at low frequencies
  • Overlaps with many MBHB signals
  • Not removable by traditional noise subtraction
  • Affects parameter estimation accuracy

Long-Duration Observations

  • Signals observable for months to years
  • Computational cost of waveform generation increases
  • Data management and processing challenges
  • Requires efficient inference methods

Multi-Source Overlapping

  • Many simultaneous resolvable sources
  • Global fitting required for accurate parameters
  • Individual source analysis must be fast
  • Scalability critical

2. Transformation Mapping Innovation

Addressing Time-Dependent Response

The key innovation tackles Taiji’s orbital motion:

Problem

  • Detector response function: R(t, θ, φ) depends on observation time t and sky location (θ, φ)
  • Neural network must learn this time dependence
  • Increases model complexity significantly
  • Requires training data covering all observation times

Solution: Coordinate Transformation

  • Maps data observed at any time to canonical “first day” configuration
  • Transformation leverages detector geometry and orbital mechanics
  • After mapping, time dependence effectively removed
  • Network trains on simplified first-day data only

Mathematical Framework

  • Detector response: h(t) = R(t, θ, φ) × h_source
  • Transformation: h_canonical = T(h(t), t, θ, φ)
  • Neural network: p(θ|h_canonical) learned on canonical data
  • Inference: Apply T to map any-time data to canonical frame, then use network

Benefits

  • Dramatically reduces training data requirements
  • Improves generalization to arbitrary observation times
  • Accelerates training convergence
  • Enables practical deployment

3. Multimodality in Arrival Time

Discovery

The analysis reveals novel multimodal structure in arrival time parameter:

Physical Origin

  • Doppler shift from detector orbital motion
  • Signal arrives at different times depending on sky location
  • Orbital motion creates periodic modulation
  • Multiple sky location hypotheses can explain same arrival time pattern

Implications

  • Traditional analyses may miss or inadequately sample these modes
  • Normalizing flows naturally capture multimodality
  • Important for accurate uncertainty quantification
  • Affects downstream astrophysical inference

Characterization

  • Bimodal or trimodal structures common
  • Separation between modes: hours to days
  • Mode weights depend on signal-to-noise ratio and sky location
  • Captured in posterior samples from flow model

Methodology

Massive Black Hole Binary Signals

Source Parameters

  • Total mass: 10⁵ to 10⁷ solar masses
  • Mass ratio: 1:10 to 1:1
  • Spins: Aligned, magnitude 0-0.9
  • Sky location: Full sky coverage
  • Distance: Gpc scales (redshift z ~ 1-15)
  • Observation duration: Months to years

Waveform Modeling

  • Inspiral-merger-ringdown phenomenological models
  • Post-Newtonian inspiral for early times
  • Numerical relativity-informed merger and ringdown
  • Detector response in Time-Delay Interferometry (TDI) channels

Data Simulation and Preprocessing

Noise Modeling

Instrumental Noise

  • Taiji design sensitivity curve
  • Shot noise, acceleration noise, other instrumental contributions
  • Frequency-dependent power spectral density

Confusion Noise

  • Galactic binary foreground
  • Simulated using population synthesis
  • Realistic amplitude and frequency distribution
  • Included in training and testing data

Data Preparation

  • Time-series or frequency-domain representation
  • Whitening using total noise PSD (instrumental + confusion)
  • Bandpassing to relevant frequency range
  • Transformation to canonical frame using mapping

Normalizing Flow Architecture

Feature Extraction Network

Input Processing

  • Multi-channel TDI data (A, E, T channels or X, Y, Z)
  • Convolutional layers for time-frequency features
  • Attention mechanisms for long-duration signals
  • Compression to feature vector

Flow Model Design

Coupling Layers

  • Rational quadratic spline transformations
  • More flexible than affine couplings
  • Better handling of complex distributions
  • Alternating variable ordering

Conditioning

  • Feature vector from extraction network
  • Conditional transformations depend on data
  • Learns mapping from data to posterior

Base Distribution

  • Multivariate Gaussian in parameter space
  • Diagonal covariance for simplicity
  • Easily sampled for inference

Training Strategy

Dataset

  • Simulated MBHBs with known parameters
  • Confusion noise realizations
  • Diverse parameter coverage
  • Canonical frame data (first day)

Loss Function

  • Negative log-likelihood
  • Maximizes probability of true parameters given data
  • Regularization for smooth transformations

Optimization

  • Adam optimizer with learning rate decay
  • Batch training for efficiency
  • Early stopping on validation set
  • Hyperparameter tuning via grid search

Inference Procedure

Parameter Estimation Pipeline

  1. Input: Observed Taiji data at arbitrary time t
  2. Transformation: Map to canonical frame using T(h(t), t)
  3. Feature Extraction: Process through trained network
  4. Flow Sampling: Sample z ~ N(0, I), transform to θ via inverse flow
  5. Output: Posterior samples p(θ|data)
  6. Computational Time: Seconds for thousands of samples

Generalization

  • Training on first-day data
  • Inference on any-day data via transformation
  • No retraining required
  • Robust across observation periods

Results

Validation in Confusion Noise

Scenario

  • MBHB signal embedded in realistic confusion noise
  • Signal-to-noise ratio: 10-100
  • Comparison with nested sampling (gold standard)

Posterior Comparison

Intrinsic Parameters

  • Chirp mass: Excellent agreement (<0.5% difference)
  • Mass ratio: Consistent within uncertainties
  • Spins: Captured distributions and correlations

Extrinsic Parameters

  • Sky location: Degree-level accuracy
  • Distance: 10-30% uncertainties, matching nested sampling
  • Inclination: Well-recovered
  • Polarization: Consistent

Temporal Parameters

  • Arrival time: Multimodal structure captured
  • Multiple peaks identified by flow model
  • Missed by some traditional samplers
  • Proper uncertainty quantification

Statistical Measures

  • KL divergence: <0.02 for most parameters
  • Jensen-Shannon divergence: Negligible
  • Overlap integral: >0.95 for 1D marginalized posteriors

Computational Performance

Speed Comparison

  • Nested Sampling: 24-72 hours on computing cluster
  • Normalizing Flow: 1-5 seconds on single GPU
  • Training Time: 2-3 days (one-time, amortized)
  • Speed-up Factor: ~10⁴ to 10⁵

Scalability

  • Constant inference time regardless of posterior complexity
  • Parallel sampling: Thousands of posterior samples simultaneously
  • Enables global fitting: Analyze hundreds of sources
  • Feasible for mission operations

Multimodality Characterization

Arrival Time Posterior

Unimodal Cases

  • High SNR, certain sky locations
  • Single dominant peak
  • Both methods agree

Multimodal Cases

  • Moderate SNR, specific sky configurations
  • Two or three peaks separated by hours to days
  • Flow model captures all modes
  • Some traditional samplers miss secondary modes or inadequately sample

Impact on Astrophysics

  • Multi-messenger follow-up: Need all possible arrival time windows
  • Sky localization: Multimodality affects area uncertainty
  • Distance estimates: Correlated with arrival time modes

Robustness Tests

Parameter Space Coverage

  • Mass range: 10⁵ to 10⁷ M☉ total mass
  • Various mass ratios and spins
  • Full sky locations
  • Different observation times during mission
  • SNR: 10-100

Noise Variations

  • Different confusion noise realizations
  • Time-varying instrumental noise (future capability)
  • Glitches and data gaps (preliminary tests)

Waveform Systematics

  • Training on approximate waveforms
  • Testing on higher-fidelity models
  • Robustness to model mismatch (ongoing)

Impact

For Taiji Mission

Operational Necessity

  • Rapid parameter estimation critical for mission success
  • Global fitting of all resolvable sources requires speed
  • Confusion noise mitigation via accurate source characterization
  • Real-time alerts for multi-messenger observations

Science Enabling

  • Population studies of MBHBs
  • Cosmological distance measurements
  • Tests of general relativity with multiple events
  • Multi-band observations coordinating with ground-based detectors

Data Analysis Pipeline

  • Integration into official Taiji analysis software
  • Low-latency parameter estimation
  • Preliminary alerts followed by refined analysis
  • Support for various source types (EMRIs, galactic binaries)

For Space-Based GW Astronomy

Methodological Advances

  • Transformation mapping generalizable to LISA, TianQin
  • Handling time-dependent responses in other missions
  • Confusion noise treatment applicable broadly
  • Sets standard for rapid inference in space

International Collaboration

  • Methods shareable across LISA, Taiji, TianQin communities
  • Benchmark for comparison studies
  • Facilitates joint data analysis efforts

For Machine Learning in Physics

Domain Adaptation

  • Transformation mapping as physics-informed preprocessing
  • Reduces model complexity via domain knowledge
  • Generalizable strategy for time-dependent systems
  • Bridges physics and ML communities

Multimodality Handling

  • Normalizing flows excel at multimodal posteriors
  • Important for many physics applications
  • Demonstrates advantages over mode-seeking methods
  • Encourages adoption in other fields

Resources

Publication

Authors

  • Minghui Du
  • Bo Liang
  • He Wang (Corresponding author)
  • Peng Xu
  • Ziren Luo (Corresponding author)
  • Yueliang Wu

Taiji Mission Resources

Official Mission Information

  • Taiji Program: Chinese space-based GW detector
  • Launch target: ~2033-2035
  • Complementary to LISA
  • Similar science goals with some unique capabilities

Technical Specifications

  • Three spacecraft triangular formation
  • ~3 million km arm length
  • Heliocentric orbit trailing Earth
  • Ultra-stable lasers and drag-free control
  • Expected sensitivity and science targets

Data Challenges

  • Taiji Mock LISA Data Challenges
  • Test datasets for algorithm development
  • Community participation encouraged
  • Benchmarking and validation

LISA (Laser Interferometer Space Antenna)

  • ESA/NASA mission, launch ~2035
  • Similar configuration and science
  • Collaboration opportunities

TianQin

  • Chinese mission, geocentric orbit
  • Different arm length and targets
  • Complementary observations

Multi-Mission Synergy

  • Joint observations for better sky localization
  • Cross-validation of detections
  • Enhanced parameter estimation
  • Broader frequency coverage

Software and Tools

Waveform Generation

  • Phenomenological MBHB models
  • Post-Newtonian codes
  • Numerical relativity catalogs

Detector Response

  • TDI (Time-Delay Interferometry)
  • Orbital mechanics simulation
  • Response function calculations

Normalizing Flows

  • PyTorch/TensorFlow implementations
  • Spline coupling layers (nflows library)
  • GPU acceleration

Comparison Tools

  • Nested sampling: MultiNest, PolyChord
  • MCMC: emcee, PyMC
  • Posterior comparison utilities

Future Directions

Method Extensions

  • Full 15D parameter space (precessing spins)
  • Eccentric orbits
  • Multi-source global fitting
  • Improved confusion noise mitigation

Additional Sources

  • Extreme mass ratio inspirals (EMRIs)
  • Galactic binaries (verification sources)
  • Stochastic backgrounds
  • Cosmological signals

Operational Integration

  • Real-time processing pipelines
  • Alert systems for electromagnetic follow-up
  • Automated quality control
  • Mission operations support

Hybrid Approaches

  • Flow-assisted MCMC
  • Refinement of flow posteriors with sampling
  • Combining speed of flows with traditional accuracy
  • Best of both worlds

Uncertainty Quantification

  • Out-of-distribution detection
  • Model confidence estimation
  • Waveform systematic uncertainty
  • Noise model uncertainties
Gravitational Waves Normalized Flow AI Taiji MBHB Inference
He Wang
He Wang
Research Associate

Knowledge increases by sharing but not by saving.