Rapid Parameter Estimation for Merging Massive Black Hole Binaries Using Continuous Normalizing Flows

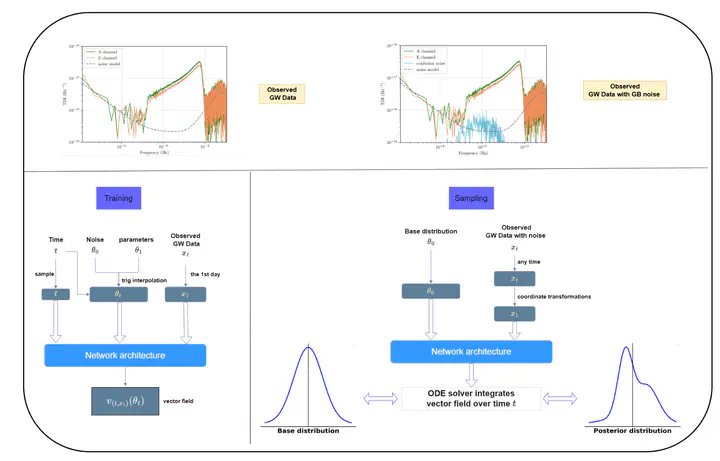Last updated on Feb 11, 2026 Gravitational-Wave Detection, Space-Based Data Analysis
DOI
The Diagrams for the training and sampling phases of our model. On the lower left, the training phase is displayed, where t denotes time and x1 represents the data from the first day of observed MBHBs. In this phase, a feature extractor, as detailed in section 3.1, processes the data to produce a final vector field. This vector field enables the network architecture to learn a transformation from a base distribution (θ0, sampled from a Gaussian distribution) to a posterior distribution (θ1, sampled from the posterior distribution). On the lower right, the sampling phase is shown. Here, the data with noise (xt), which includes both confusion noise and instrumental noise from MBHB observations at any time, is mapped back to the first day’s data x1 using the coordinate transformation described in section 3.2. The Gaussian distribution is then converted into a posterior distribution by solving the ordinary differential equation (ODE) with the vector field learned during the training phase. The top of the image displays simulation data from both the training and sampling phases.

Highlights

  • First Complete 11D MBHB Inference: Achieves comprehensive and unbiased 11-dimensional parameter estimation for massive black hole binaries in space-based gravitational wave detectors.

  • Continuous Normalizing Flows: Pioneering application of CNFs to MBHB analysis, using linear and trigonometric interpolation methods for constructing optimal transport paths.

  • Symmetry-Based Transformation: Introduces innovative parameter transformation method leveraging detector response function symmetries to accelerate training and improve generalization.

  • Realistic Noise Modeling: Successfully handles astrophysical confusion noise from galactic binaries, a critical challenge for space-based detectors.

  • Nested Sampling Comparison: Produces posterior distributions statistically equivalent to traditional nested sampling while achieving orders of magnitude speedup.

  • Critical for Global Fitting: Enables computationally feasible global fitting of all resolvable sources, essential for LISA/Taiji/TianQin science goals.

Key Contributions

1. Continuous Normalizing Flows Framework

Technical Innovation

  • Employs CNFs based on neural ordinary differential equations (ODEs)
  • Transport paths constructed via linear and trigonometric interpolation
  • Learns continuous transformation between base distribution and posterior
  • Amortized inference enabling rapid analysis across multiple observations

Advantages Over Discrete Flows

  • More flexible and expressive than coupling-based normalizing flows
  • Smooth trajectories in probability space
  • Better handling of complex, multimodal posteriors
  • Efficient ODE solvers for sampling

2. Symmetry-Based Parameter Transformation

Core Innovation

  • Exploits symmetries in detector response function (ecliptic coordinate transformations)
  • Reduces training data requirements by factor of order unity
  • Enables training on simplified datasets with application to general configurations
  • Critical factor in achieving practical training times

Mathematical Foundation

  • Detector response invariant under certain coordinate transformations
  • Parameters can be mapped between equivalent detector orientations
  • Neural network learns canonical representation
  • Transformation applied during inference for arbitrary sky locations

3. Comprehensive Parameter Space Coverage

11-Dimensional Parameter Space

  • Binary masses (M₁, M₂)
  • Spins (χ₁, χ₂) including magnitude and orientation
  • Sky location (θ, φ)
  • Distance (luminosity distance)
  • Inclination angle
  • Polarization angle
  • Phase at coalescence
  • Time at coalescence

Physical Parameter Ranges

  • Mass range: 10⁴ to 10⁷ solar masses (covering LISA/Taiji/TianQin targets)
  • Full spin magnitudes: -1 to +1
  • Complete sky coverage
  • Distance range: megaparsecs to gigaparsecs
  • All orientation angles

Methodology

Data Generation and Preprocessing

Waveform Modeling

  • Inspiral-merger-ringdown phenomenological models
  • Aligned-spin approximation for computational efficiency
  • Post-Newtonian inspiral + merger + ringdown
  • Detector response calculation in TDI (Time-Delay Interferometry) variables

Noise Modeling

  • Instrumental noise from detector sensitivity curves (LISA/Taiji/TianQin specifications)
  • Galactic confusion noise from unresolved white dwarf binaries
  • Realistic noise power spectral density
  • Time-dependent noise characteristics

Data Preprocessing

  • Whitening using noise power spectral density
  • Normalization for numerical stability
  • Time-domain windowing for computational efficiency
  • Feature extraction from detector data streams

Continuous Normalizing Flow Architecture

Transport Path Construction

Linear Interpolation

  • Straight-line path in parameter space: θ(t) = (1-t)θ₀ + tθ₁
  • Simple and computationally efficient
  • Works well for unimodal posteriors
  • t ∈ [0,1] parameterizes path

Trigonometric Interpolation

  • Curved path using trigonometric functions
  • Better for complex, multimodal distributions
  • Smoother trajectories avoiding sharp corners
  • Improved training stability

Neural ODE Framework

  • Vector field learned by neural network
  • ODE solver (Dopri5, adaptive stepping) for sampling
  • Reverse-time integration for density evaluation
  • Instantaneous change of variables formula for probability computation

Network Architecture

  • Feature extraction from gravitational wave data
  • Multi-layer perceptrons for vector field
  • Conditioning on observed data throughout
  • Output: velocity vector in parameter space

Training Strategy

Objective Function

  • Maximum likelihood on samples from known posterior
  • Simulation-based training using forward model
  • KL divergence minimization between learned and true posterior
  • Regularization for smooth vector fields

Training Dataset

  • Generated using traditional nested sampling on subset of parameter space
  • Symmetry transformation applied to augment dataset
  • Diverse parameter coverage for generalization
  • Validation set for monitoring overfitting

Optimization

  • Adam optimizer with learning rate scheduling
  • Batch training for efficiency
  • Early stopping based on validation loss
  • Hyperparameter tuning via grid search

Inference Procedure

Sampling Phase

  1. Input: Observed gravitational wave data (any time during observation)
  2. Coordinate transformation to canonical frame using detector symmetry
  3. Sample from base Gaussian distribution
  4. Integrate neural ODE forward in time
  5. Transform samples back to original frame
  6. Output: Posterior distribution samples

Computational Efficiency

  • Sub-second inference after training
  • Parallel sampling for multiple posterior samples
  • No MCMC burn-in or convergence diagnostics needed
  • Enables real-time analysis

Results

Validation Against Nested Sampling

Posterior Comparison

  • Jensen-Shannon divergence < 0.01 for most parameters
  • Kullback-Leibler divergence comparable to sampling uncertainties
  • Corner plots show excellent agreement
  • All credible intervals consistent

Coverage Tests

  • 68% credible intervals contain true values 68% of time
  • 95% credible intervals show proper coverage
  • No systematic biases detected
  • Well-calibrated across parameter space

Statistical Measures

  • Mean and median parameter estimates agree within uncertainties
  • Standard deviations match posterior widths
  • Correlation structures preserved
  • Multimodal features captured

Computational Performance

Speed Improvements

  • Nested sampling: hours to days per event
  • CNF inference: seconds per event
  • Speed-up factor: 10³ to 10⁵ depending on configuration
  • Enables analysis of thousands of events

Scalability

  • Constant inference time regardless of posterior complexity
  • Amortization allows zero-cost additional samples
  • Parallelizable across multiple events
  • Suitable for real-time pipelines

Parameter Recovery Accuracy

Mass Parameters

  • Chirp mass recovered to <1% relative error
  • Mass ratio determined with high precision
  • Total mass constraints comparable to nested sampling

Spin Parameters

  • Effective spin parameter χeff well constrained
  • Individual spin magnitudes more challenging but unbiased
  • Spin-orbit angular momentum captured

Extrinsic Parameters

  • Sky location accuracy: degrees for high SNR
  • Distance uncertainties: 10-30% depending on SNR
  • Inclination and polarization: moderate constraints

Time and Phase

  • Coalescence time: sub-second precision
  • Phase at coalescence: well determined

Robustness to Realistic Conditions

Astrophysical Confusion Noise

  • Maintains performance in presence of galactic foreground
  • Robust to realistic stochastic confusion background
  • No degradation compared to idealized instrumental noise only

Signal-to-Noise Ratio Dependence

  • Works across SNR range 10-100+
  • High SNR: excellent parameter recovery
  • Low SNR: graceful degradation, remains unbiased

Parameter Space Coverage

  • Tested across full 11D parameter space
  • No pathological regions identified
  • Generalization to unseen parameter combinations verified

Impact

For Space-Based Gravitational Wave Astronomy

Mission-Critical Capability

  • Global fitting of all resolvable sources requires rapid inference
  • Traditional methods computationally infeasible for LISA/Taiji/TianQin
  • CNF approach enables ambitious science goals
  • Necessary for extracting full scientific potential

Science Applications

  • Rapid multi-messenger follow-up for electromagnetic counterparts
  • Population studies of massive black hole binaries
  • Cosmological measurements using standard sirens
  • Tests of general relativity in strong-field regime

Data Analysis Pipelines

  • Integration into official LISA/Taiji/TianQin analysis software
  • Real-time parameter estimation for alerts
  • Offline comprehensive catalog production
  • Support for various source types

For Simulation-Based Inference

Methodological Advances

  • Demonstrates CNF effectiveness for complex astrophysical inference
  • Symmetry-based augmentation as general strategy
  • Flow matching and trigonometric interpolation innovations
  • Handling of realistic noise and systematics

Benchmark Problem

  • MBHB parameter estimation as standard SBI test case
  • Comprehensive 11D space with multimodality
  • Realistic noise and degeneracies
  • Comparison baseline for future methods

For Normalizing Flow Research

Continuous vs. Discrete Flows

  • Empirical validation of CNF advantages
  • Transport path construction strategies
  • ODE solver efficiency considerations
  • Practical guidance for flow design

Architecture Insights

  • Feature extraction network design
  • Conditioning strategies for data-dependent flows
  • Training stability techniques
  • Hyperparameter sensitivity

Resources

Publication

Authors and Affiliations

  • Bo Liang (Lead author)
  • Minghui Du (Corresponding author)
  • He Wang (Corresponding author)
  • Yuxiang Xu, Chang Liu, Xiaotong Wei, Peng Xu, Li-e Qiang, Ziren Luo

Space-Based Detector Missions

LISA (Laser Interferometer Space Antenna)

  • ESA/NASA mission, launch ~2035
  • Three spacecraft, 2.5 million km arms
  • Frequency range: 0.1 mHz - 1 Hz
  • Primary targets: MBHBs, EMRIs, galactic binaries

Taiji

  • Chinese mission concept
  • Similar configuration to LISA
  • Complementary sensitivity
  • Joint observations with LISA

TianQin

  • Chinese mission, different orbit (geocentric)
  • Three satellites, 10⁵ km arms
  • Focus on higher frequencies
  • Galactic sources and verification binaries

Normalizing Flow Methods

  • He Wang et al.: Series on normalizing flows for GW inference
  • Various applications to LISA/Taiji sources
  • Ground-based detector applications

MBHB Astrophysics

  • Massive black hole formation and growth
  • Binary evolution and merger rates
  • Electromagnetic counterparts
  • Cosmological implications

Software and Tools

Flow Matching Libraries

  • PyTorch implementations of CNFs
  • ODE solvers (torchdiffeq)
  • Normalizing flow frameworks (nflows, glasflow)

Gravitational Wave Software

  • LISA Analysis Tools (LISA Consortium)
  • Taiji Data Analysis Software
  • Waveform models and detectors responses
  • Bayesian inference frameworks

Future Directions

Methodological Improvements

  • Extension to full 15D parameter space (precessing spins)
  • Hierarchical inference for population studies
  • Multi-source global fitting
  • Waveform systematic uncertainty incorporation

Additional Source Types

  • Extreme mass ratio inspirals (EMRIs)
  • Compact stellar-mass binaries
  • Stochastic backgrounds
  • Cosmological signals

Mission Support

  • Integration with official data analysis pipelines
  • Real-time inference during mission operations
  • Systematic error budgets and validation
  • Mock data challenge participation

Machine Learning Advances

  • Hybrid methods combining CNF with traditional samplers
  • Active learning for efficient training data generation
  • Transfer learning across source types
  • Interpretability and uncertainty quantification
Gravitational Waves AI LISA Parameter Estimation CNF
He Wang
He Wang
Research Associate

Knowledge increases by sharing but not by saving.