Lecture 12. Generative Models
Table of Contents
CS231n 课程的官方地址:http://cs231n.stanford.edu/index.html
该笔记根据的视频课程版本是 Spring 2017(BiliBili),PPt 资源版本是 Spring 2018.
1. Supervised vs Unsupervised Learning

2. Generative Models
生成式模型是无监督学习范畴下的一类模型。在给定训练数据的情况下,我们任务的目标是从相同的数据分布中生成新的样本。那么我们有一些训练数据是由某种分布 $p_{\text{data}}(x)$ 中生成的,然后我们想从中习得一个模型 $p_{\text{model}}(x)$ 来以相同的分布生成样本。

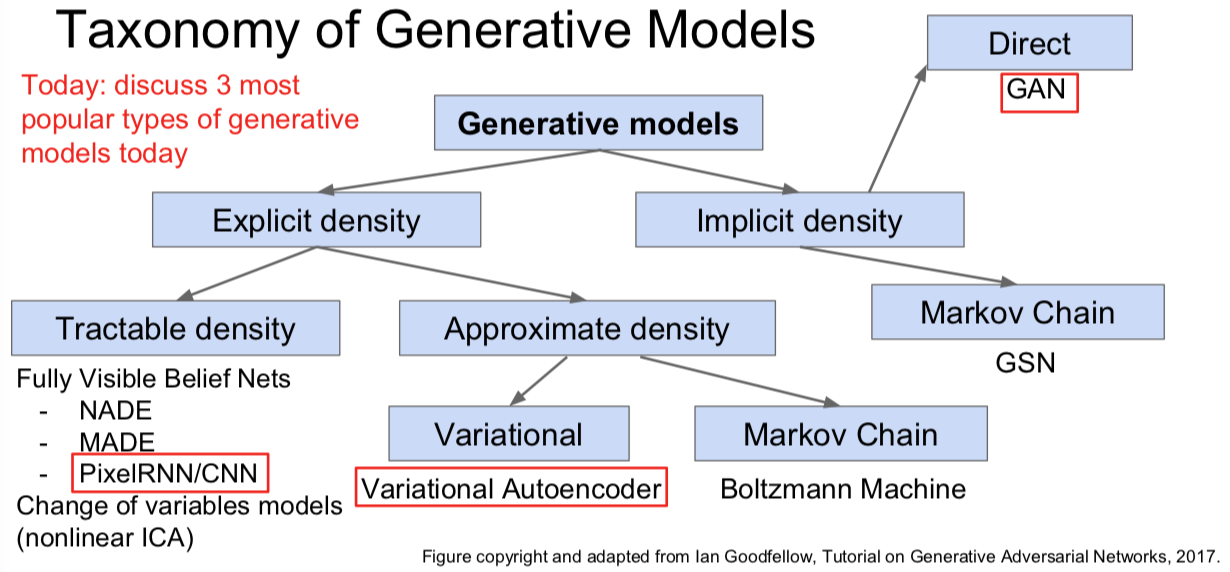
生成式模型可以解决密度估计问题,也就是我们之前看到的估计训练数据的潜在分布的任务。这也是无监督学习的 核心问题。同时,我们将会看到该问题的一些特点:
我们可以用生成式模型来做显式的密度估计。在这种情况下我们会显式地定义并求解出目标模型 $p_{\text{model}}$ 。
我们也可以进行隐式的密度估计。这种情况下我们会习得一个能够从 $p_{\text{model}}$ 中生成样本的模型而不需要显式地定义它。
Why Generative Models?
- 我们能够从数据分布中创造出我们想要的真实样本。
- 我们还可以用时间序列数据的生成式模型来进行仿真和规划,这样一来就能在强化学习应用中派上用场。
- 隐式表征的推断成为可能。学习隐式特征对于下游任务(在这里可以作为一般特征)来说是非常有用的。
2.1 PixelRNN and PixelCNN
[van der Oord et al. 2016]
PixelRNN 和 PixelCNN 都属于全可见信念网络(fully visible belief networks),它们要做的就是对一个密度分布显式建模。那么在这种情况下,我们有图像数据 $x$,同时我们想要对该图像的概率分布或者似然 $p(x)$ 建模。对于这几种模型,我们使用链式法则将这一似然分解为一维分布的乘积。那么这里我们有每个像素 $x_i$ 的条件概率,其条件是给定所有下标小于 i 的像素 $(x_1,\dots,x_{i-1})$ 。这时图像中所有像素的概率或者联合概率就是所有这些像素点——所有这些似然的乘积。
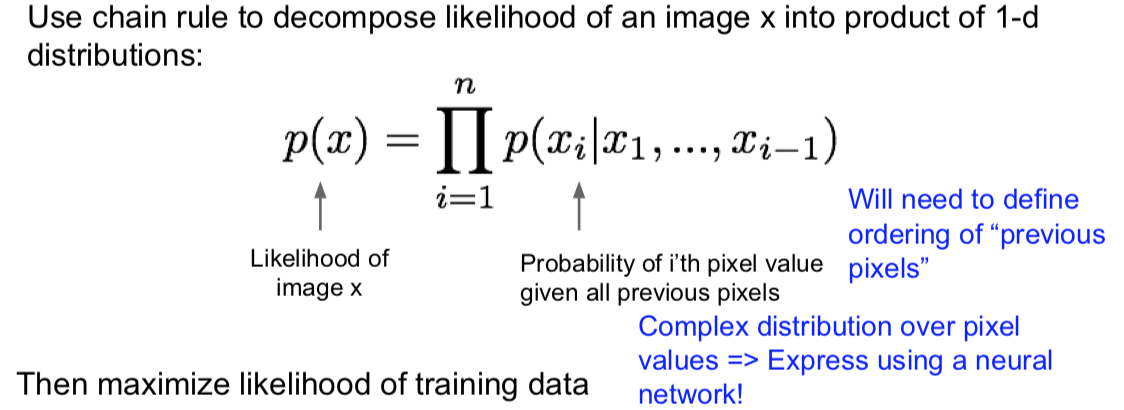
一旦我们定义好这一似然,为了训练这一模型我们只要在该定义下最大化我们的训练数据的似然。
那么如果我们观察下右边的像素值概率分布,也就是给定所有在 $x_i$ 之前的像素值条件下的条件概率 $p(x_i)$ ,那么我们该如何建模呢?
我们之前已经了解到如果想要进行一些复杂的变换,我们可以利用神经网络实现这一切。神经网络是一种表达复杂变换的很好的方法。所以我们家下来会做的就是我们会只用一个神经网络来表达这一关于概率分布的复杂函数。
不过在这里你会遇到的一个问题是:即使我们打算用神经网络解决问题,我们也必须考虑如何对这些像素排序。我们曾说过在这一任务中我们有一个给定所有之前的像素,关于 $x_i$ 的分布 $p$ ,但是究竟什么是所有之前的像素呢?
PixelRNN

PixelCNN
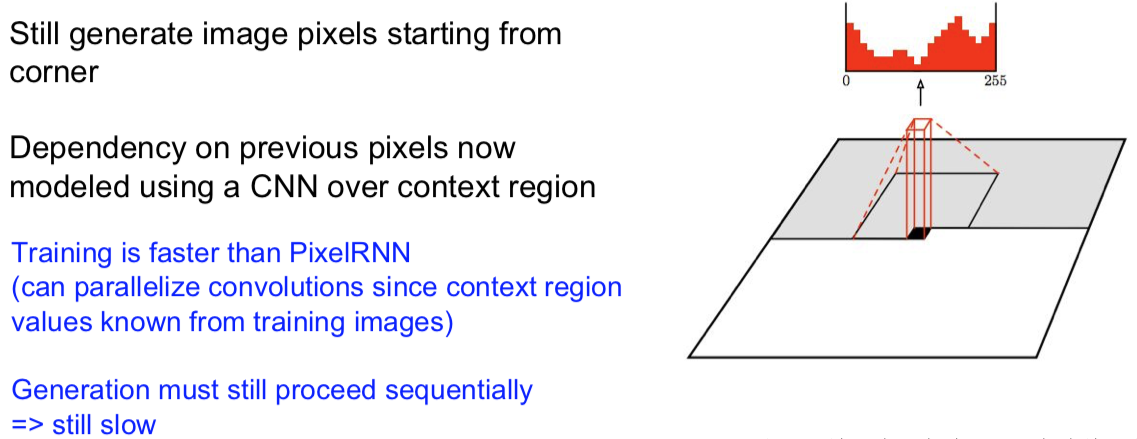
Summary for PixelRNN and PixelCNN

So far…

2.2 Variational Autoencoders (VAE)
对于 VAEs(变分自编码器),我们将会定义一个不易处理的密度函数,我们要通过附加的隐变量 z 对其(密度函数)建模。我们的数据的似然 $p(x)$ 现在是下面等式右边的积分形式,也就是对所有可能的 z 值取期望: $$ p_\theta(x) = \int p_\theta(z)p_\theta(x|z) dz $$ 这时我们就看到问题了,我们不能直接优化它,所以我们只能转而找出一个似然函数的下界,然后再对该下界进行优化。
接下来,先回顾下什么是自动编码器(Autoencoders)。
Autoencoders
Encoder
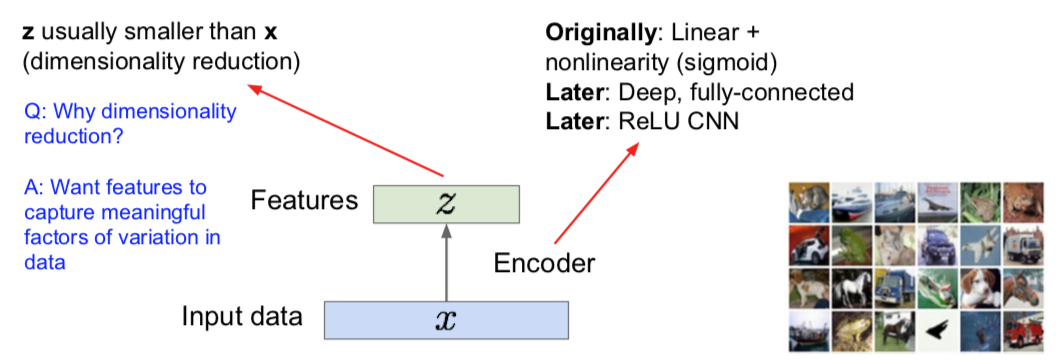
Decoder
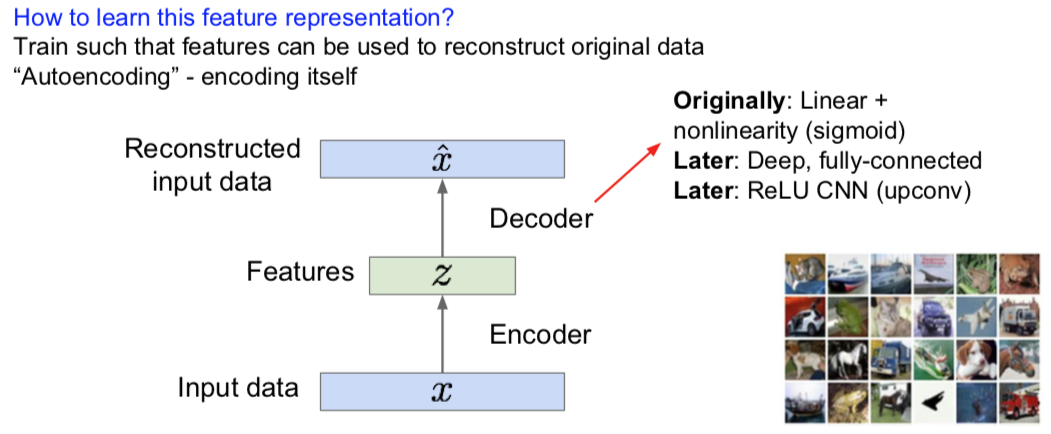
记得把 L2 损失用起来。。。。
事实上解码器可以用一个监督模型作为训练起始:
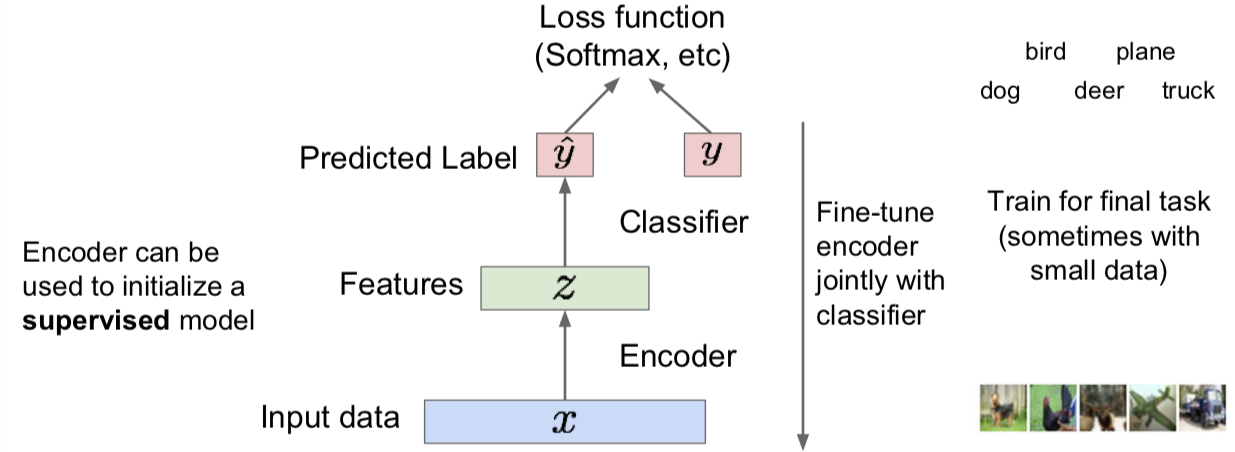
既然自编码器能重构数据,也可以从一个监督模型起始学习到特征,那么可以用它生成新数据么?
Variational Autoencoders
此处一篇 paper:
Kingma and Welling, “Auto-Encoding Variational Bayes”, ICLR 2014
变分自编码器!这是通过向自编码器中加入随机因子获得的一种模型。这样一来我们就能从该模型中采样从而生成新数据。
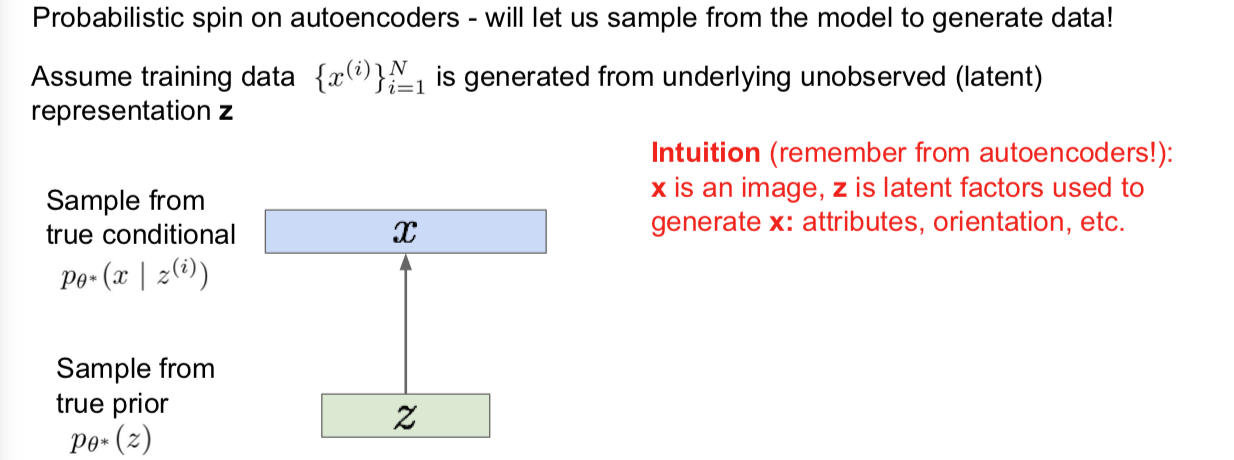
我们有 x 而 i 的范围是从 1 到 N。该数据是从某种潜在的不可观测的隐式表征 z 中生成的。那么从直观上讲,z 的元素要捕捉的信息是在训练数据中某种变化因子的多少。那么这就像是在说它们(z 中的元素)可能是某种类似于属性的东西,比如说我们打算生成一些面孔(图像),那这时候它(z 的元素)就有可能指代脸上有几分笑意,也可以指代眉毛或者头发的位置,也可以是头部的朝向。这些都有可能隐变量学习的。那么我们的生成过程就是要从关于 z 的先验分布中采样,对于某种属性,比如有几分笑。我们都可以假设一个我们觉得它应该是怎样一个先验分布,高斯分布就是一个对 z 中每个元素的一个自然的先验假设。同时我们将会通过从在给定 z 的条件下,x 的条件概率分布中 p(x|z) 中采样。那么我们先对 z 采样,也就是对每个隐变量采样,接下来我们就可以利用它并从这里对图像 x 采样。

对于上述采样过程,真实的参数是 theta*。我们有关于先验假设和条件概率分布的参数。同时我们的目的在于获得一个生成式模型,从而利用它来生成新的数据。真实参数中的这些参数是我们想要估计并得出的。
我们先来谈谈该如何表示上述模型。如果我们要对该生成过程建模,事实上我们之前已经说过我们可以选一个简单的关于 z 的先验分布,比如高斯分布什么的,同时隐变量也选的合理。对于给定 z 的 x 的条件概率分布 p(x|z),事实上它更复杂一些,因为我们要用它来生成一个图像。那么 p(x|z) 像我们之前看到的那样,当我们需要想要表示一个复杂函数的时候,我们可以用神经网络来表示,也就是说,用神经网络来对 p(x|z) 建模是一个很自然的选择。

这时候,我们就要调用该解码器网络了。那就是说,我们想要选取隐式表征并将其解码为它所表示的图像。
那我们要如何训练这个模型呢?我们想要训练好该模型,这样一来就能习得一个对于这些参数的估计。如果你还记得训练生成式模型的策略,也就是回到那些完全可见信念网络(fully visible belief networks),如我们的 pixelRNNs 和 CNNs,一个直接且自然的策略就是通过最大化训练数据的似然函数来寻找这些模型的参数。之前我们看到过,在这种情况下在已经给定隐变量 z 的情况下,我们需要写出 x 的分布 p 并对所有可能的 z 值取期望。因为 z 是连续的,所以这里我们有这样一个表达式。在隐变量 z 下,我们的公式是这样的。
现在我们想要最大化它的似然,那么会有什么问题呢?我们可以直接通过求导来最大化似然吗?不。这个积分不会很好解。那咋整?
Variational Autoencoders: Intractability

上面是我们的数据似然项,第一项是 z 的分布 p(z),这里我们之前说过可以直接把它设定为简单的高斯分布;对于 p(x|z) 我们之前说要指定一个神经网络解码器,这样一来,任意给定一个 z,我们就能获得 p(x|z),这也就是神经网络的输出。但是!我们想要对每一个 z 值计算 p(x|z),现在还是很困难的,所以我们无法计算该积分。

那么数据的似然函数是难解的,结果就是它直接导致了模型的其他项。我们来看后验密度分布,也就是 p(z|x),(根据贝叶斯公式)也就等于 p(x|z) 乘以 p(z) 再除以 p(x),这也是难解的,我们现在有 p(x|z) 以及 p(z),但是 p(x) 也就是我们的似然函数,也就是这个积分很难计算。
所以我们无法直接优化它(似然),不过我们会看到一个解决办法,一个可以让我们训练该模型的办法,那就是:如果在使用神经网络解码器来定义一个对 p(x|z) 建模神经网络的同时,我们现在额外定义一个编码器 q(z|x),我们会把这成为编码器,因为我们打算将输入 x 编码为 z,从而得到似然 p(z|x)。也就是说,我们定义该网络来估计出 p(z|x)。没错,这个后验密度分布项仍然是难解的。如果我们用该附加网络来估计该后验分布,我们将会看到这事实上将使得我们得到一个数据似然的下界,而该下界是易解的,也是能优化的。
Details
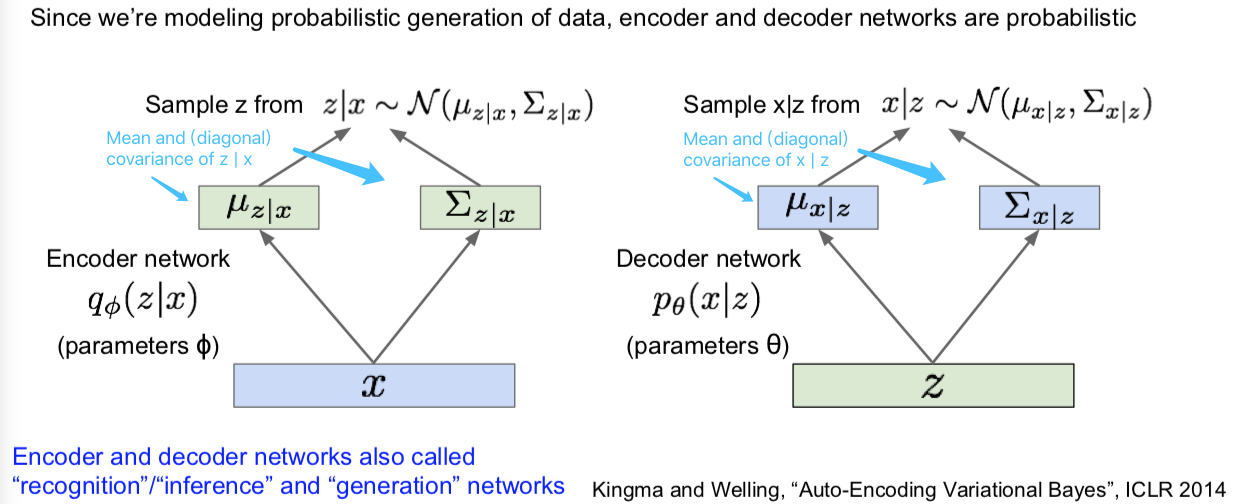
那么对于我指出的这些编码器和解码器说得再具体一点就是:在变分自编码器中,我们想要得到一个生成数据的概率模型。在讲自编码器的时候我们已经讲过这一概念,就是说,将输入 x 送入编码器得到一些特征 z,然后通过解码器网络再把 z 映射回到图像 x。所以这里我们还是有一个编码器网络和一个解码器网络,但是我们要将一切随机化。那么现在我们的参数是 $\phi$,解码器网络 q(z|x),将会从这里输出一个均值和一个对角协方差矩阵。这些将会由编码器网络直接输出,同时对于解码器网络也一样,只不过它是从 z 开始,将会输出均值和关于 x 的对角协方差矩阵。给定 z 下,这里的 x 的维度和输入一样。该解码器网络由不同的编码器网络的参数 $\theta$ 决定。
现在为了真正得到 z,准确地讲是给定 x 下的 z 和给定 z 下的 x,我们将会从这些分布(p 和 q)中采样。那么现在我们的编码器和解码器网络,所给出的分别是 z 和 x 的(条件概率)分布,并会从这些分布中采样从而获得值。现在你应该已经了解采样和生成新数据的整个流程了。
还有一点要注意的是,这些编码器和解码器网络还有其他的叫法。编码器网络也是一种识别或者推断网络(recognition or inference network),因为我们是在给定 x 的条件下形成对隐式表征 z 的推断的,而对于解码器网络,我们将用来执行生成过程,所以你也会听到有人称它生成网络(generation network)。

既然已经配备编码器和解码器网络,下面我们再来求解下数据似然。这里我们会使用对数似然。
那么我们将会看到,如果我们想获得 log(p(x)),我们可以把它写成 p(x),但要关于 z 取期望。所以 z 是采样自分布 q(z|x),也就是我们目前为止通过编码器网络定义的分布。我们之所以能这么做,是因为 p(x) 并不依赖 z,z 不是它的一部分。现在关于 z 取期望的作用之后就能显现出来了(第一行)。
根据贝叶斯共识,从这一原始表达式开始(第二行),我们可以将其展开成 p(x|z) 乘以 p(z) 再除以 p(z|x) 的对数形式。下面为了求解它我们可以再乘一个常数,也就是乘以 q(z|x) 除以 q(z|x),事实上只是乘了常数1(第三行)。这样一来,我们要做的就是把它写成三项之和的形式,这里的关键在于使用对数法则(第四行)。当我们仔细观察这三项,会发现第一项是 log(p(x|z)) 关于 z 取期望,接下来我们还会有两个 KL 项,实际上是 KL 散度项,它们是用来描述这两个分布有多么相似,也就是分布 q(z|x) 和分布 p(z) 有多相似,这事实上就是上面的(第二个)期望项,是对分布函数距离的度量。

接下来我们将会看到我们之前见过这些是能够写出的性质很好的 KL 项。现在如果我们再仔细观察这三项,第一项是由 p(x|z) 它由解码器提供,同时我们能够通过采样计算并估计出这些项的值,而且我们还会看到我们能够通过一种叫做重参数化(re-parametrization)的技巧来进行一次可微分的采样。如果你对重参数化感兴趣可以参考那篇论文。现在只要知道我们能够计算就行了,然后这些 KL 项里面,第二个 KL 项是两个高斯分布之间的 KL 散度,也就是我们的 q(z|x),还记得是我们的编码器生成了一个均值和一个协方差么?它们构成了一个性质很好的高斯分布。同样,接下来我们的先验假设 p(z) 也是一个高斯分布。那么这样你有一个关于两个高斯分布的 KL 散度时,就等于你获得了一个很好的闭式解(closed form solution)。下面这第三个 KL 项是一个关于 q(z|x) 和 q(z|x) 的 KL 散度。但是我们知道 p(z|x) 是一个难解的后验概率,我们之前看到过,我们不想直接计算它,这也是为什么我们用 q 来估计它。那么这一项仍然是一个问题,那么这一项仍然是一个问题。

但是关于这第三项,我们目前所了解的是 KL 散度是对两个分布之间距离的度量,从定义上看它总是大于或等于零。因此我们能对它做的是,在前面我们有两项很好的解决,这两项合起来就是一个搞的定的下界,我们就可以对其取梯度并进行优化。p(x|z) 是可微分的,而这一 KL 项(也就是这个闭式解)也是可微分的,同时这是一个下界,因为我们知道右边的 KL 项,也就是难解的那一个是大于等于零的,于是我们就有了一个下界。

那么为了训练一个变分自编码器,接下来我们要做的是转而优化并最大化这一下界。因此我们是在优化数据似然的下界。这就意味着我们的数据总是有一个至少和这个我们要最大化的下界一样大的似然。这样一来,我们想要找到参数 $\theta$,通过估计参数 $\theta$ 和 $\phi$ 我们才可以最大化这一似然。
最后一个对于这一下界的直观解释是,其中第一项对所有采样的 z 取期望,z 是 x 经过编码器网络采样得到的,对 z 采样然后在所有的 z 值取 p(x|z) 的期望,这就是重构(reconstruction)。这实际上就是在说,如果我想让它变大,也就是让 p(x|z) 变大,这样一来就有点像是在最大限度地重构数据,所以和之前的自编码器一样。但这第二项是要让 KL 散度变小,让我们的近似后验分布和先验分布逐渐变得相似。这就意味着我们想让隐变量 z 遵循我们期望它遵循的分布类型和形状。
- Q:为什么将先验假设也就是隐变量分布设定为高斯分布?
- 原因在于我们是在定义某种生成过程,该过程首先要对 z 采样然后对 x 采样。把它假设为高斯分布是因为这是一种合理的先验模型。对于隐变量的属性来说,分布成某种高斯分布是讲得通的,而且这么做可以让我们接下来能够优化模型
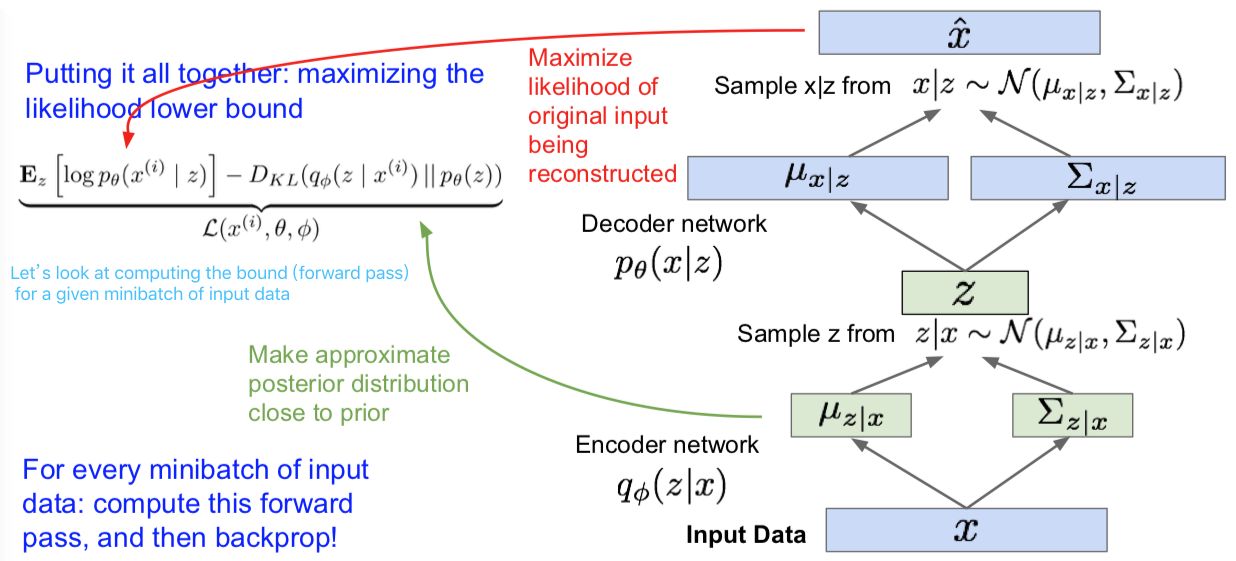
我们刚才讲的是我们如何得出该下界。现在我们把这些东西整理到一起,然后再把训练 AE(自动编码器)的流程过一遍。上图左上的公式就是我们要优化以及最大化的下界。现在对于前向传播来说,我们要按下面的流程处理。我有输入数据 x,我们会有小批量的输入数据。然后我们把它传递经过编码器网络,我们会得到 q(z|x)。我们会通过 q(z|x) 来计算 KL 项。然后我们会根据给定的 x 的 z 分布对 z 进行采样,由此一来,我们就获得了隐变量的样本,这些样本可以根据 x 推断获得。之后,我们继续把 z 传给第二个解码器网络。通过这个解码器网络,我们会获得 x 在给定 z 的条件下的分布的两个参数:均值和协方差。然后最终我们就可以在给定 z 的条件下从这个分布中采样获得 x,这里就会产生一些样本输出。我们在训练的时候,我们就是要获得该分布,而我们的损失项将会是给定 z 的条件下对训练像素值取对数。那么我们的损失函数要做的是就是最大化被重构的原始输入数据的似然。
现在,对于每个小批量输入,我们都要计算这一前向传播过程,取得所有我们所需的项。它们都是可微分的,所以我们接下来把它们全部反向传播回去并获得梯度。我们利用梯度不断更新我们的参数,包括生成器以及解码器,网络参数 $\theta$ 和 $\phi$ 从而最大化训练数据的似然。
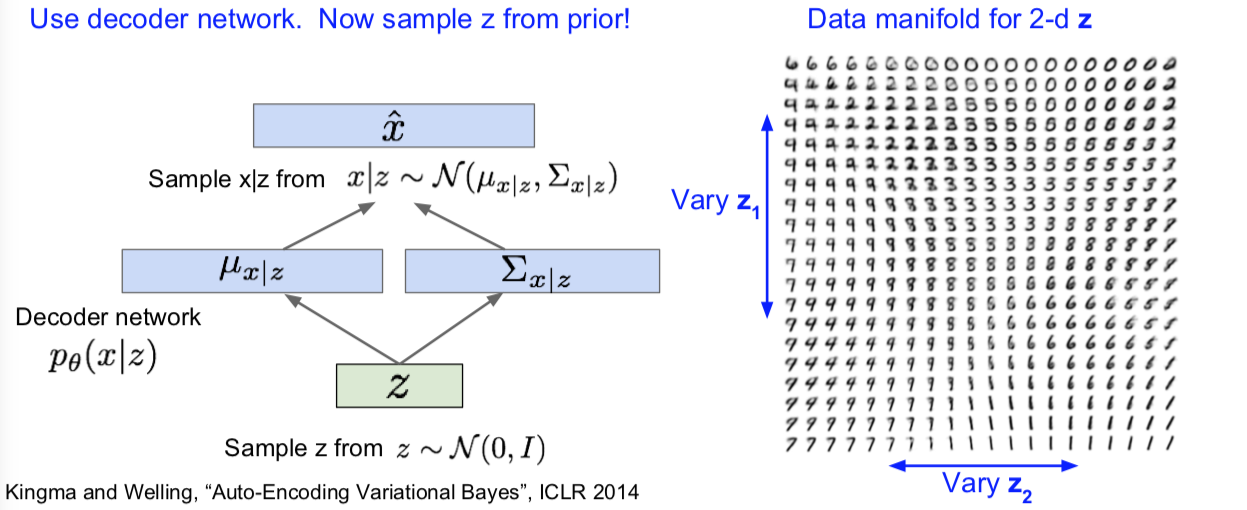
那么一旦我们训练好 VAE。要想生成数据,我们只需要用解码器网络就可以了。现在我们在训练阶段就可以开始对 z 采样,而不用从后验分布中采样。在生成阶段,我们会从真实的生成过程中采样。因此,我们从设定好的先验分布中采样,然后接下来我们就要从这里对数据 x 采样。
右图就是在 MNIST 数据集上训练的 VAE。我们可以生成这些手写数字样本。我们之前说过,用 z 表示隐变量,这样一来,由于我们是从先验分布的不同部分采样的,所以我们可以通过改变 z 来获得不同的可解释的意义。关于二维 z 的数据流形,如果我们有一个二维的 z 然后我们让在某个区间内变化,比如该分布的百分比区间。接下来我们让 z1,z2 逐渐变化,那么从图上你就可以看到各种不同的 z1 和 z2 的组合所生成的图像(光滑地过渡变化)。
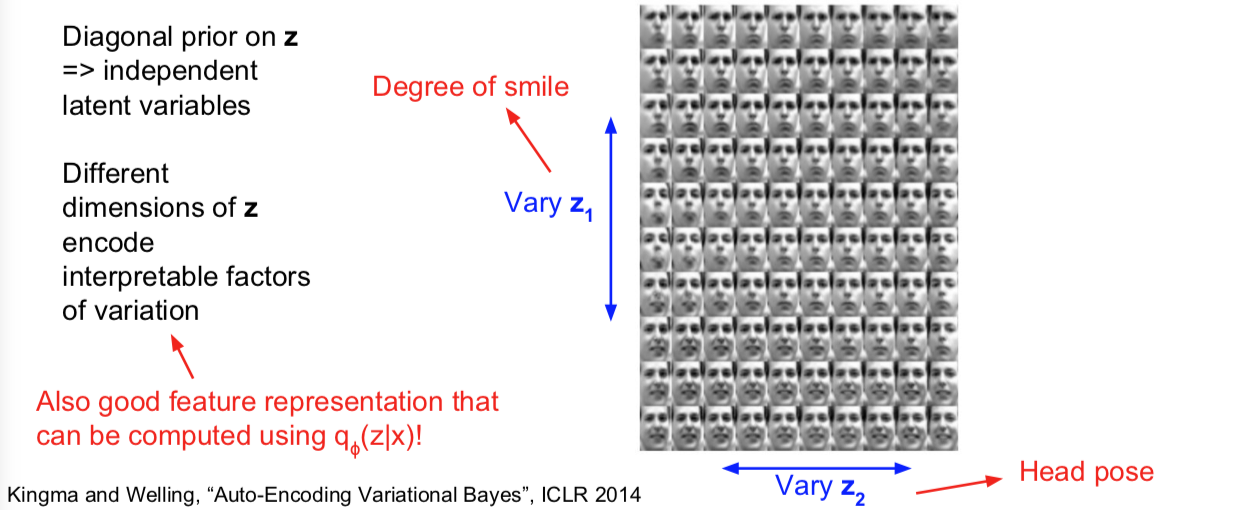
我们对 z 的先验假设是对角的,这样做是为了促使它成为独立的隐变量,这样一来它才能编码,具有可解释性的变量。因此,我们就有了 z 的不同维度。它们编码了不同的具有可解释性的变量(看人脸图)。
还有一点需要指出的是,这么做的好处就是这些 z 同时也是很好的特征表征。因为他们编码了这些不同的可解释的语义信息的多少。那么这样一来,我们就可以利用 q(z|x),也就是我们训练好的编码器,我们给它一个输入图像 x,我们可以将之映射到 z,并把 z 用作下游任务的特征,比如监督学习,就像分类任务或者其他任务。
Pros vs Cons

2.3 Generative Adversarial Networks (GANs)

我们目前见过的模型中 pixelCNNs 还有 pixelRNNs 定义了一个易处理的密度函数,可以通过它们优化训练数据的似然。作为对比,VAEs 有这么一个额外的定义在生成过程中的隐变量 z。有了 z 的话,就可以获得许多我们讲过的有利的性质,不过同时我们也因此获得了一个难解的密度函数,对于该函数我们不能直接优化,所以我们推导出了一个似然函数的下界,然后转而对它进行优化。
那么现在如果我们放弃显式地对密度函数建模会怎么样呢?事实上我们想要获得的能力其实只是从分布中采样并获得质量良好的样本。那么这就是 GANs 所采用的方法。在 GANs 中,我们不再在显式的密度函数上下功夫,而是采用一个博弈论的方法,并且模型将会习得从训练分布中生成数据,而这一实现是基于一对博弈玩家的。

此时一篇 paper:
Ian Goodfellow et al., “Generative Adversarial Nets”, NIPS 2014
那么,在 GAN 的配置中,我们真正在意的是我们想要能够从一个复杂的高维训练分布中采样。如果想从这样的分布中生成样本是没有什么直接的方法可以采用的。换句话说,该分布十分复杂,我们无法从中采样。因此我们将要采用的方案是:从一个简单点的分布中采样,比如随机噪声,高斯噪声就可以被用来做这件事。那这样一来,我们所要做的就是习得一个从这些简单分布直接到我们想要的训练分布的一个变换。
那么问题来了,要用什么来表示这一复杂变换呢?当然是神经网络啦!当我们想要对某些复杂的函数或者变换建模的时候,神经网络都是一个不错的选择!接下来对于 GAN 的准备工作还要做的是取得一些具有某一指定维度的噪声向量作为输入,然后我们要把该向量传给一个生成器网络,之后我们要从训练分布中采样并将结果直接作为输出。那么对于每一个随机噪声输入,我们都想让它和来自训练分布的样本一一对应。
Training GANs: Two-player game
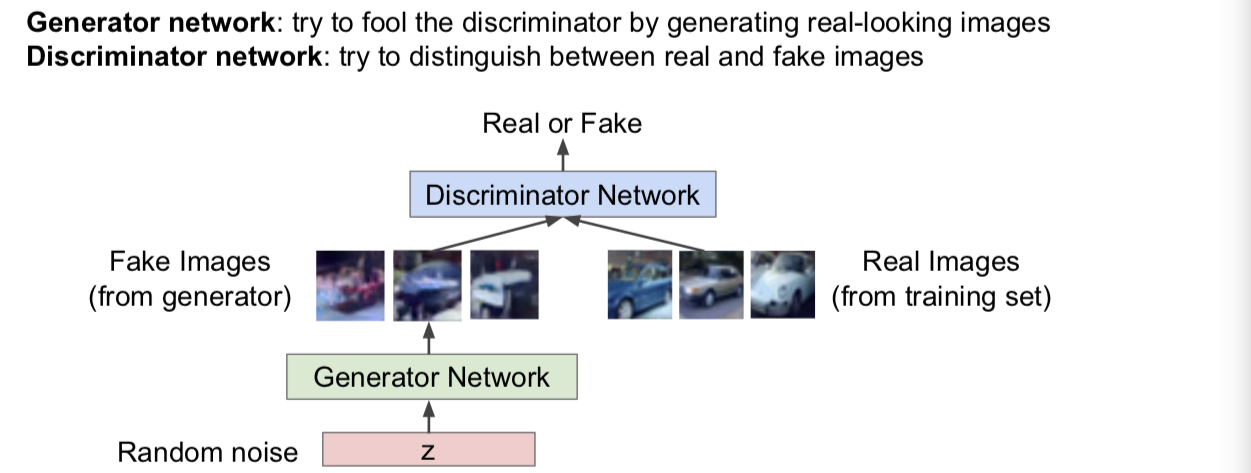
我们接下来训练这个网络的方式是我们会把训练过程看作两个玩家博弈的过程。我们有两个玩家,一个是生成器网络,还有一个额外的判别器网络。我们的生成器网络作为玩家1会试图骗过判别器网络,欺骗的方式就是生成一些看起来十分逼真的图像,同时我们的第二个玩家,也就是判别器网络,将要试图把真实图片和虚假图片区别开来。那么判别器网络会尽可能地正确的指出哪些样本是生成器网络生成的赝品。
那么这就看起来,我们将随机噪声输入到生成器网络,而生成器网络将会生成这些图像,我们称之为来自生成器的伪样本。然后我们会从训练集中取一些真实图片,这时我们希望判别器能够对于每个图片样本区分是真实样本还是伪样本。我们的想法是:如果能够获得一个很好的判别器,也就是说我们想训练一个性能良好的判别器,如果它能很好地区分真实样本和伪造样本,同时,如果我们的生成器能够生成一些伪造样本,而且这些伪造样本能够成功地骗过判别器那么我们就获得了一个很好的生成式模型。如此一来,我们将可以生成一些看起来很像训练集合中的图像的样本。

好,那么我们现在有两个玩家,然后我们要通过一个 minimax 博弈公式联合训练这两个网络。那么该 minimax 目标函数就是上面的公式。我们的目标是要让目标函数在 $\theta_g$ 上取得最小值,$\theta_g$ 是指生成器网络 g 的参数,同时要在 $\theta_d$ 上取得最大值,$\theta_d$ 指的是判别器网络的参数。仔细观察这些项,会发现它所表达的是:第一项是在训练数据的分布上取 $\log(D(x))$ 的期望。这一项的 $\log(D(x))$ 是判别器网络在输入为真实数据(训练数据)时的输出,该输出是真实数据从分布 $p_{data}$ 中采样的似然概率;第二项是对 z 取期望,而 z 是从 $p(z)$ 中采样获得的,这意味着从生成器网络中采样,同时 $D(G(z))$ 这一项代表了以生成的伪数据为输入的判别器网络的输出,也就是判别器对于生成器网络生成的数据给出的判定结果。
对于该过程的解释是:我们的判别器的目的是最大化目标函数,也就是在 $\theta_d$ 上取得最大值。这样一来 $D(x)$ 就会接近1,也就是使判别结果接近真,因而该值对于真实数据应当很高。这样一来 $D(G(z))$ 的值也就是判别器对伪造数据的输出就会相应减小,我们希望这一值接近于0。因此,如果我们能够最大化这一结果,就意味着判别器能够很好地区别真实数据和伪造数据,换句话说,就是更好地对真实数据和伪造数据进行分类。下面,对于生成器来说,我们希望它最小化该目标函数,也就是说让 $D(G(z))$ 在这里接近于1,那么用1减去它就会很小,这事实上也就是我们所期望的。如此一来,判别器网络就会把伪造数据视为真实数据,那也就意味着,我们的生成器正在生成真实样本。这就是需要我们好好理解的 GANs 的目标函数。
- Q:我们究竟该如何给数据打上标签或者说如何训练这些网络。
- 这是一个无监督学习模型,所以不会有打上标签的数据。但是从生成器网络中生成的数据,也就是这些伪造图像的标签是0或假,而我们的训练集都是真实图片,因为会被标记为1或是真。那么当我们有了这些以后,对于判别器的损失函数而言就会使用这些信息,判别器要做的就是对生成器生成的函数输出0,而对真实图像输出1,那么这其中是没有外部标签的。
- Q:判别器网络输出的是生成器网络的标签吗?
- 事实上,生成器网络并不是真的做分类,它的目标函数是公式里的 $D(G(z))$,它想要这个值尽可能高,因此给定一个固定的判别器,它会想要习得生成器的参数,这样的话才能达到目标。那么我们会取一个固定的判别器输出,然后用它来进行反向传播。

我们首先对判别器进行梯度上升,从而习得 $\theta_d$ 来最大化该目标函数,接着对生成器进行梯度下降。对 $\theta_g$ 进行梯度下降可以达到最小化目标函数的目的,这时候的目标函数只取右边的一项,因为只有这一部分和 $\theta_g$ 有关。
那么 GAN 就是这样训练的,我们可以交替训练判别器和生成器,每次迭代,生成器都在试图骗过判别器。但是在实践中,有一件事不得不注意,那就是我们定义的生成器目标函数并不能够工作的很好。至于原因,我们需要看下损失函数的函数空间。如果我们仔细看看关于 $D(G(z))$ 的损失函数的函数空间,如果我们在这里用1减去 $D(G(z))$,也就是我们期望对于生成器能够最小化的项,它的形状如上图所示。那么我们想要最小化该函数,不过我们发现该损失函数的斜率越往右走越大,$D(G(z))$ 越是接近1,该函数的斜率就越高,也就是能很好地骗过判别器的时候,我们才会获得大的梯度值。另一方面,当生成器生成的样本并不怎么样的时候,也就是生成器还没能习得如何生成良好的样本的时候,这也正是判别器能够轻易地将样本判别为伪造的时候,这个时候的梯度也就相对平坦。这事实上意味着梯度信号主要受到采样良好的区域支配,然而事实上我们真正想要的是在采样效果并不好的时候多学到一些知识。我们想要的就是从训练样本中习得知识。

那么这样一来就使得学习很艰难,所以为了提高学习效率,我们接下来要做的是针对梯度定义一个有一点不同的目标函数,也就是我们转而去做梯度上升算法,也就是说我们不再最小化判别器判别正确的概率,也就是我们之前的做法,而是将这一过程反转,转而进行最大化判别器出错的概率。那么这样一来就会产生一个关于最大化的目标函数,也就是最大化 $\log(D(G(z)))$ 。那么现在这里应该有一个负号在这里,但是我们现在想要最大化这个反转了的目标函数。现在如果我们在上 面右边画出这一函数,那么我们就可以在左侧生成样本质量还不是很好的时候,获得一个很高的梯度信号。现在更平坦的区域转到了右边,也就是我们的样本已经很好的时候,如此一来,我们就会在生成样本质量不是很好的时候学到更多的知识。
在这样的情况下,我们仍有相同的目标函数,其目的仍然是骗过判别器,不过现在的它要比之前你表现更好,而且事实上很多这种普通 GAN 公式(目标函数)的研究用的就是这种目标函数。
另一方面,联合训练这两个网络是十分有挑战性的,而且会不稳定。那么就像我们在这里看到的,我们需要通过交替地训练判别器网络与生成器网络来完成训练过程。由于这种交替训练的方式,模型不可能一次性训练两个网络。还有一个问题就是损失函数的函数空间会影响训练的动态过程。因此有一个活跃的研究领域仍然是如何选择目标函数,从而获得更好的损失函数空间来帮助训练并使其更加平稳。

那么现在我们把讲过的东西都放在一起,看看完整的 GAN 训练算法到底是什么样子。(在训练中)我们所要做的就是在每一个训练迭代期,我们都要先训练判别器网络,然后才是生成器网络。对于判别器网络的 k 个训练步,我们将会从噪声先验分布 z 中采样得到一个小批量样本,接着同样从训练数据 x 中采样获得小批量的真实样本。那么下面我们要做的是,将噪声样本传给生成器网络,并在(生成器)输出端获得伪造图像,那么也就是说我们有一个小批量的伪造图像和小批量的真实图像。然后我们会用这样的小批量数据在判别器上进行一次梯度计算,接下来(利用梯度信息)更新判别器参数,按照这样的步骤迭代一定的次数来训练一会判别器。在这之后,我们会执行第二步,也就是训练生成器。在这一步我们会采样获得一个小批量噪声样本,将它传入生成器,然后对生成器进行后向传播,从而优化其目标函数。总之,我们想让生成器尽可能骗过判别器。
因此,我们要交替进行上述两个步骤,也就是交替地在判别器和生成器上计算梯度。我之前说训练判别器的时候要进行 k 步(梯度计算),事实上这是一个有争议的话题,有些人认为在判别器上迭代一次就可以了,最好是是判别器上迭代一步,生成器上迭代一步;有的人认为,训练判别器的迭代次数最好多于训练生成器的步数,然而对此并没有明确的规则。人们发现在不同的问题上有不同的技巧来提高效果。我想指出的是,已经有一些近期的研究减缓了这一问题带来的麻烦,也就是说,你不需要在花太大的力气在研究如何平衡两种网络的训练步数上面。这样一来会使得训练更加稳定同时带来更好的结果,Wasserstein GAN 就是一个例子,它是一项达成前述目标的一项重要工作。
此处的 paper:
Arjovsky M, Chintala S, Bottou L. Wasserstein gan[J]. arXiv preprint arXiv:1701.07875, 2017.
Gulrajani I, Ahmed F, Arjovsky M, et al. Improved training of wasserstein gans[C]//Advances in Neural Information Processing Systems. 2017: 5767-5777.
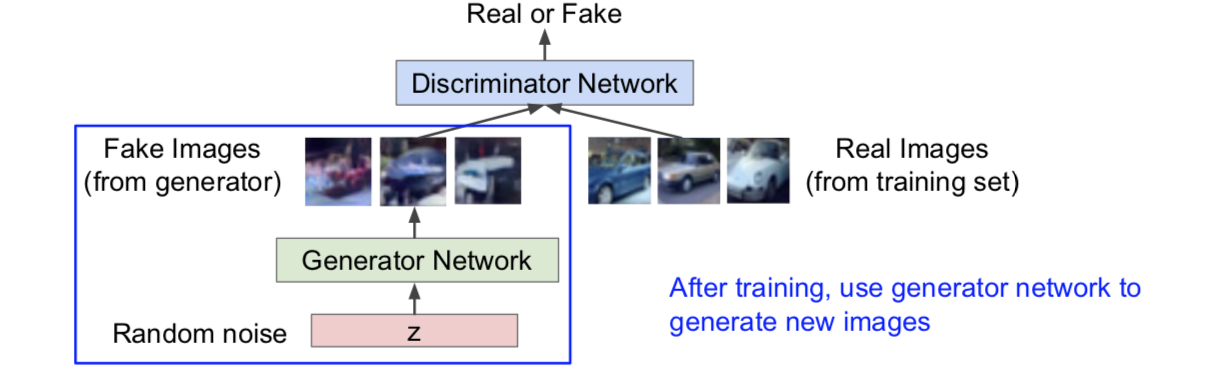
现在看看目前为止的整个训练图景。我们配置有神经网络,也对生成器网络和判别器网络都进行了训练。现在在几轮训练之后,我们就可以取得生成器网络并用它来生成新的图像,我们只需要把噪声 z 传给它,并生成伪造图像。
GANs 生成的样本:


Generative Adversarial Nets: Convolutional Architectures
此处一篇 paper:
Radford et al, “Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks”, ICLR 2016

自 Goodfellow 之后就开始陆续出现了一些改善 GANs 的研究。对于提升样本质量的重大飞跃是由 Alex Radford 在 ICLR2016 上提出的,他提出给 GANs 增加卷积结构。在该文章中,有整整一个系列的结构设计指南,来帮助 GANs 生成更好的样本。下面具体讲讲:
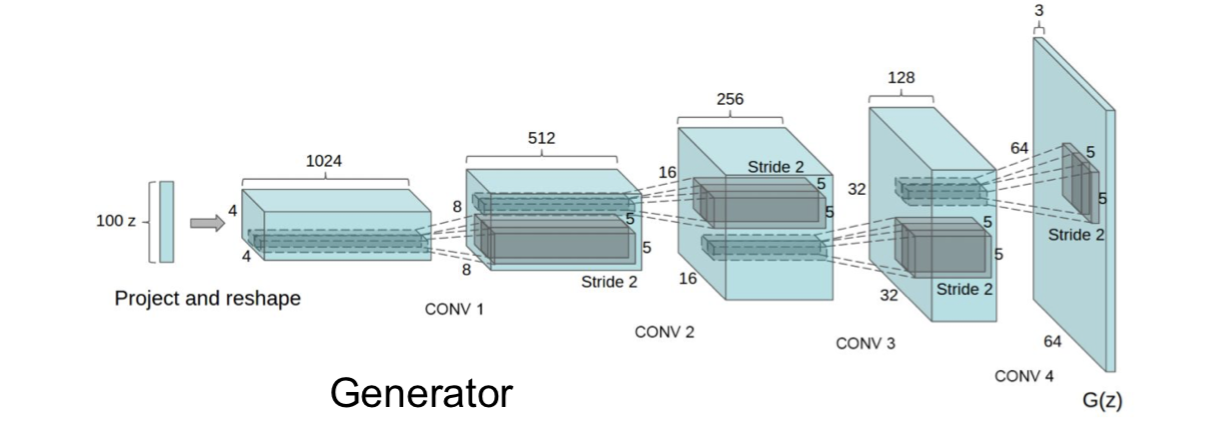
这是论文中使用的一个卷积结构的例子。从输入 z 开始,也就是噪声向量 z,接着一路变换直到输出样本。

那么通过这样一个大型的卷积结构,我们会看到从这样的模型生成的样本才真正开始具有好的视觉质量。那么这些样本是通过在卧室数据集上训练得来的,同时我们可以看到各种各样看上去非常真实的卧室,家具等等。

我们也可以试着解释一下这些 GANs 都在做些什么。本例中,我们可以做的是:我们可以取得两个 z,也就是两个不同的噪声向量,然后我们在这两个向量之间插值。这里每一行都是一种从随机噪声 z 到另一个随机噪声向量 z 的插值过程。你可以看出来它在变化,这些都是平滑插值产生的图像。
Generative Adversarial Nets: Interpretable Vector Math
我们可以做得另一件事是,我们要更深入分析这些向量 z 的含义,也就是说我们可以对这些向量做一些数学运算。图中的实验所做的是取得一些笑脸图像,采样自女性笑脸,然后我们再取一些淡定脸的女性样本,再取一些淡定脸男性样本,我们会得到笑脸男性样本。那么我们可以取得一个由上述公式产生的 z 向量,然后生成并获得笑脸男性样本。

下面一样意思。。。。

2017: Explosion of GANs

此处两个很帅气的链接:

Summary: Pros vs Cons

2.4 Recap
