Lecture 14. Deep Reinforcement Learning
Table of Contents
CS231n 课程的官方地址:http://cs231n.stanford.edu/index.html
该笔记根据的视频课程版本是 Spring 2017(BiliBili),PPt 资源版本是 Spring 2018.
- 书籍推荐:
By Richard S. Sutton and Andrew G. Barto 《Reinforcement learning An introduction》
很新 2018版
By Dimitri P. Bertsekas and John Tsitsiklis《Neuro-Dynamic Programming》
比较老,经典
By Sebastian Thrun 《Probabilistic Robotics》
不太算强化学习,但很好
1. What is Reinforcement Learning?
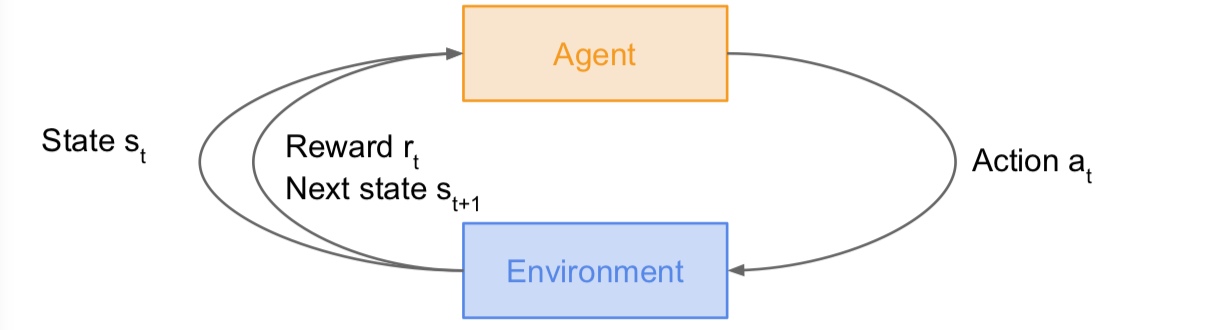
我们有一个代理和一个环境,环境赋予代理一个状态,反过来,代理将采取行动,然后环境将回馈一个奖励。下一个状态也是如此。这一过程将会继续循环下去,一次一次进行,直到环境给出一个终端状态,结束这个环节。
例子1:Cart-Pole Problem

例子2:Robot Locomotion
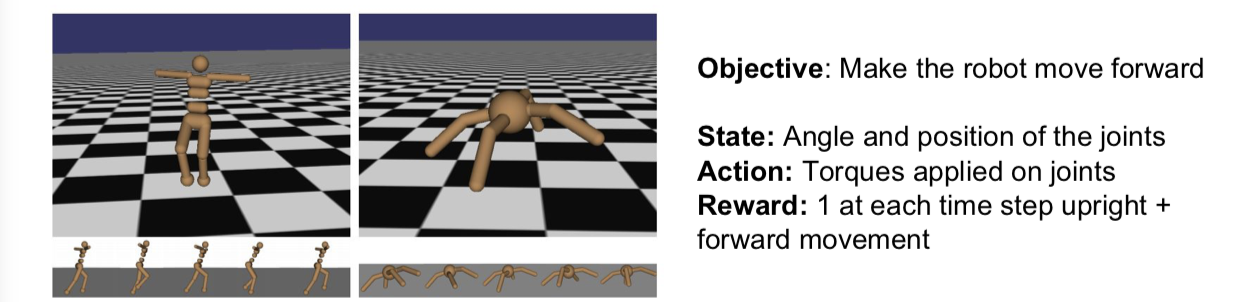
例子3:Atari Games

例子4:Go
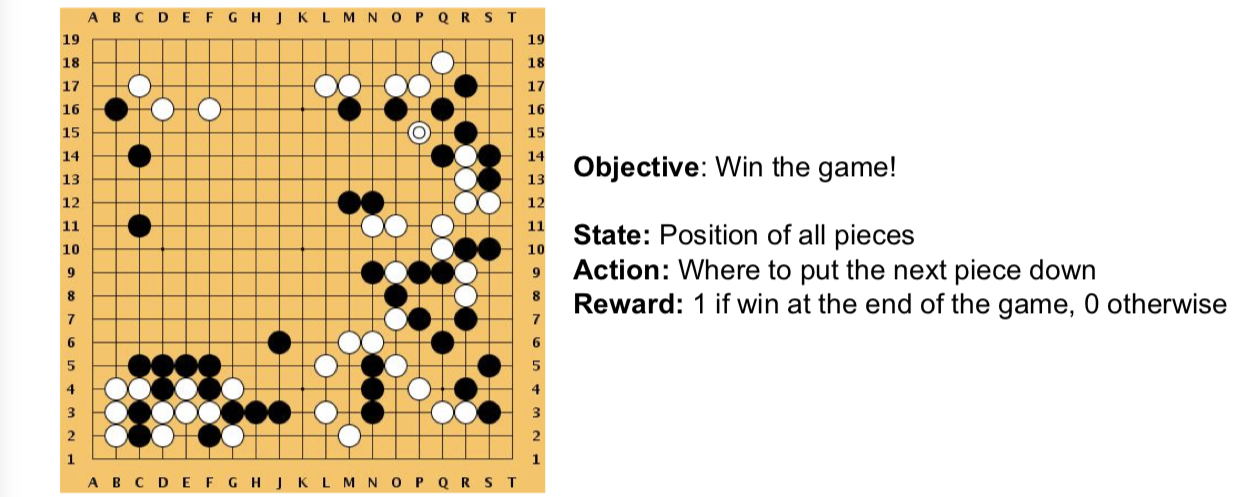
2. Markov Decision Processes (MDP)

事实上,一个马尔科夫决策过程就是强化学习问题的数学表达。马尔科夫决策过程满足 Markov 性,即当前状态完全刻画了世界的状态。MDP 由一组对象定义,这个对象元组中有 S,也就是所有可能状态的集合;元组中还有 A,所有运动的集合;同时还有 R,也就是奖励的分布函数,给定一个状态一组行动,于是它就是一个从状态行为到奖励的函数映射;还有 P,表示下一个状态的转移概率密度分布是给定一个状态行为组将采取的动作;最后有一个 gamma,折扣因子,它是用来对近期奖励以及远期奖励分配权重的。

因此,马尔科夫决策过程的工作方式是:令我们的初试时间步骤 t 等于零,然后环境会从初始状态分布 $p(s)$ 中采样,并将一些初始状态设为 0,然后从时间 t 等于零直到完成,我们将遍历这个循环,代理将选择一个动作 $a_t$,环境将从这里获得奖励,也就是给定状态,以及刚刚采取的行动的条件下所获得的奖励,这也是抽样下一个在时间 t+1 给定你的概率分布的状态。然后代理人将收到奖励,进入下一个状态,继续通过这个过程再次循环,选择下一个动作,以此类推,直到结束。
基于这个,我们可以定义一个策略 $\pi$,它是一个状态到行为的函数,它指定了在每个状态下要采取的行动,这可以使确定性的,也可以是随机的。而我们现在的目标是要找到你的最佳决策 $\pi^*$,最大限度地提高你的配权之后的全部奖励之和。在这里可以看到有一些未来的奖励,也可以通过折扣因子来折扣。
2.1 A simple MDP: Grid World
让我们来看一个简单的 MDP 的例子:
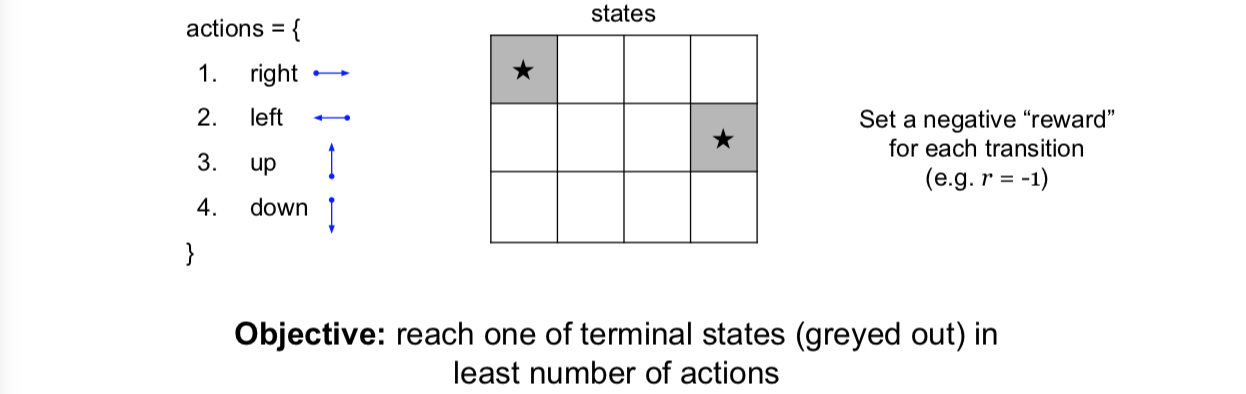
这里有网格世界,里面有网格任务的状态,你可以在网格的任意单元格中,这就是你的状态。根据你的状态采取行动,而这些行动会是简单的动作,比如向右、向左、向上或向下等。而且,每次转换或每个时间步骤都会得到一个负的奖励,你采取的每一个动作都会发生,就像 r 等于 -1。而你的目标是用最少的行动达到上面所示的灰色状态的最终状态之一。那么为了达到终端状态,所花费的时间越长,你将会积累这些负的奖励。

看一下这里的一个随机策略,一个随机策略将基本上包含在任何给定的状态或者单元格中,你只是随机抽样将要移动的方向,所有方向都有相同的概率。另一方面,我们希望拥有的最优决策基本上是采取行动,把我们推向最进阶终端状态的方向。如上图,如果我们恰好在最终的状态之一,我们应该总是朝着让我们到达这个终点的方向前进,否则,如果你在其他状态,你想要采取的方向会是将使你最接近这些状态之一。

至此,我们已经给出了 MDP 的描述,我们的目的在于找出最佳策略 $\pi^*$,最佳策略是能够最大化奖励综合的策略。最佳策略所提供的信息是在任意的给定状态下,我们应该采取什么行动来最大化我们将得到的奖励总和。
那么就有一个问题,我们如何处理 MDP 中的随机性呢?初始状态的抽样转移概率分布都是随机的,而转移概率分布会给我们下一个状态的分布等等。
我们所要做的就是最大化预期的奖励总和。比较正式地,我们可以写出最优决策 $\pi^*$,作为这个未来奖励决策的预期总和 $\pi$ 的最大化,其中我们有初始状态,它是采样于状态分布的,我们有行为,这些行为是根据我们的决策和给定状态采样的,然后我们从转移概率分布中抽取下一个状态。
2.2 Definitions: Value function and Q-value function

在我们讨论如何找到这个决策之前,我们先来谈谈一些对我们有帮助的定义。具体地说,是有值函数(value function)和 Q 值函数。所以,当我们遵循这个决策的时候,每次迭代都要采取一组行为轨迹,而且我们将把我们的初始状态设为零,$s_0,a_0,r_0,s_1,a_1,r_1$ 等等,这样我们就会得到状态、行动和奖励的轨迹。
那么我们目前的所处的状态有多好呢?任何状态下的价值函数都是从状态 s 的决策到现在的决策之后的预期积累回馈。这是从当前状态开始,期望累积奖励的期望值。
一个状态+行动组有多好呢?在状态 s 时采取行动 a 有多好呢?我们用一个 Q 值函数来定义这个问题,遵守决策的期望累积奖励,这个函数是在状态 s 下采取行动 a。
2.3 Bellman equation

那么可以得到最优 Q 值函数就是 Q*,这是我们从给定的状态动作组下得到的最大期望累积奖励。它的定义在上面面。
接下来我们将看到强化学习中的一个重要的东西,就是 Bellman 等式。我们来考虑一下这个 Q 值函数的最优策略 Q*,这个最优策略 Q* 要满足 Bellman 等式,上面就是它的定义,可以看到这也意味着给定任何状态动作组 s 和 a,这一对的价值就是你将要得到的回馈 r,再加上你最终进入的任何状态的价值,也就是 s’。既然我们知道了最佳决策,也知道要在 s‘ 状态下执行我们能做的最好的行动,那么在状态 s’ 上的值就会成为我们行动上的最大值 Q* 在 s’ 转改下的 a’。然后,我们就得到了上面的最佳 Q 值的表达式。一如既往,我们在这里有这样的期望,因为对我们将要结束的状态具有随机性。
我们也可以从这里推断出我们的最优策略就是在任何状态下按照具体的 Q* 采取最好的行动,Q* 将会告诉我们可以从我们的任何行动中获得最大的未来回馈,所以我们应该采取一个遵循这一方针的决策,然后只采取这个行为就可以带来最佳奖励。
2.4 Solving for the optimal policy

那么我们该如何求解这个最优策略?解决这个问题的一种方法就是所谓的值迭代算法,我们将通过 Bellman 方程作为迭代更新,在每一步中,我们将通过试图强化 Bellman 方程来改进我们对 Q* 的近似。在一些数学条件下,我们也知道这个序列 Q 和函数 $Q_i$ 将收敛到我们的最优 Q* 在 i 趋近于无穷的时候。
但存在什么问题呢?一个重要问题是:它是不可扩展的(not scalable)。我们必须计算每个状态动作组的 s 值,以便进行迭代更新,但这就有一个问题了,如果你看一下这些游戏的状态,比如我们谈过的 Atari 游戏,将是像素屏幕,这是一个巨大的状态空间。去计算整个状态空间是不可行的。那有什么解决办法呢?我们可以使用函数逼近器来估计 Q 的 s, a,例如,一个神经网络。之前我们已经看到,如果我们要估计一些真正的不知道的复杂函数,那么神经网络就是一个很好的估计方法。
3. Q-Learning
接下来看看 Q-learning 的形式:

我们要做的是使用函数逼近器来估计我们的动作值函数。如果这个函数逼近器是最近被使用过的,比如深度神经网络,那么这就被称为 deep Q-learning!
在这种情况下,我们也有我们的函数参数 $\theta$,所以我们的 Q 值函数是由我们的神经网络的这些权重 $\theta$ 决定的。

好,给出这个函数近似后,我们如何求解我们的最优策略?记得我们要找一个满足 Bellman 方程的 Q 函数,所以我们想要强制使这个 Bellman 方程成立了,当我们有这个神经网络逼近我们的 Q 函数时,我们可以做的是可以尝试训练这个损失函数并最小化 Bellman 方程式的误差,或者 Q(s, a) 离目标的距离(右边的 $y_i$ ),这就是之前看到的 Bellman 方程。
我们要用这些损失函数的前向传播来试图最小化这个误差,然后进行后向传递,梯度更新只会是采取中损失的梯度,就我们的网络参数的 $\theta$。所以我们的目标是产生像我们正在逐步尝试迭代使 Q 函数更接近我的目标值的效果。
来看个例子:Case Study: Playing Atari Games

3.1 Q-network Architecture
(暂时放弃治疗。。。。。)