Lecture 3. Loss Functions and Optimization
Table of Contents
CS231n 课程的官方地址:http://cs231n.stanford.edu/index.html
该笔记根据的视频课程版本是 Spring 2017(BiliBili),PPt 资源版本是 Spring 2018.
另有该 Lecture 3. 扩展讲义资料:
之前的内容已经讲了如何对每个样本图片进行线性参数化计算,最后让每个样本图片在各个分类上都有一个得分(数字)。那么如何使每一个样本的得分结果是正确的,并且要更加正确呢?这时候就需要定义损失函数(loss function) 来量化得分究竟有多么的正确,以及自动寻找最佳的参数使得损失函数的结果极值化的过程就是所谓的优化(optimization)。
小哥说了一句英文让我感觉很帅,默默的抄下来以后自己也可以用得上:
So this loss function has kind of a funny functional form, so we’ll walk through it in a bit more, in quite a bit of detail over the next couple of slides.
那么损失函数的样子还蛮有意思的,我们稍微费点心思来看看,接下来几张幻灯片里诸多细节。
很快小哥讲了一个 SVM 的多分类损失函数,企图用经典机器学习的一个简单例子让同志们了解损失函数究竟是如何计算和判断的。不过,从学生反应和弹幕的情况来看,听的人们似乎都很懵逼。。。。咱先把严格的定义抄录下来:
Loss:
Given a dataset of examples ${(x_i,y_i)}^N_{i=1}$, where $x_i$ is image and $y_i$ is (integer) label.
Loss over the dataset is a sum of loss over examples: $$ L=\frac{1}{N}\sum_iL_i(f(x_i,W),y_i) $$
1. Multiclass SVM loss
Multiclass SVM loss: (also Hinge Loss 合页损失)
Using the shorthand for the scores vector: $s=f(x_i,W)$
The SVM loss has the form: $$ \begin{array}{rl} L_i &= \sum_{j\neq y_i} \begin{cases} 0 & \text{if } s_{y_i } \geq s_j +1 \\ s_j-s_{y_i}+1& \text{otherwise} \end{cases} \\ &= \sum_{j\neq y_i}\max(0,s_j-s_{y_i}+1) \end{array} $$
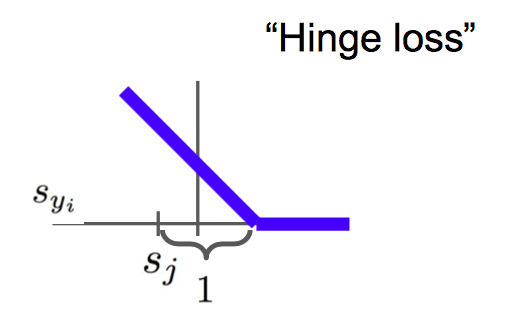
Q: 为啥合页损失里的阈值要取1?
- 其实这是可以任意选择的值。因为我们并不真正关心损失函数中得分的绝对数值,而是关心得分的相对数值,只关心正确分类能不能远远大于不正确分类的分数。所以实际上如果把整个 W 参数放大或缩小,那么所有的得分也都会相应地放大或缩小。(有详细推导)
Q: 合页损失的最大值和最小值?
- 最小值是0(对应于所有的分类里,正确的得分都非常大),最大值是无穷大。
Q: 若初始化的参数非常的小,呈现较小的均匀分布的值,于是初期所有的得分都近乎为0并且差不多相等,那么合页损失预计会如何?
- 损失函数值为分类的数量减去1.(代码调试策略,预期损失函数的值)
Q: 假如合页损失中的求和针对的是全部类别,包括 $j=y_i$,会怎样呢?
- 损失函数增加了1
Q: 假如合页损失中的求和换成为取平均值,会怎样呢?
- 不会变化。(因为取平均值和求和之间只相差一个倍数,即样本数目)
Q: 假如合页损失有一个平方操作:$ \sum_{j\neq y_i}\max(0,s_j-s_{y_i}+1)^2$,会怎样呢?
- 会变得不同。(变成非线性了)
废话不多说,直接上代码:
def L_i_vectorized(x, y, W): scores = W.dot(x) margins = np.maximum(0, scores - scores[y] + 1) margins[y] = 0 loss_i = np.sum(margins) return loss_i
1.1 Regularization
接下来的问题就很有趣了,关于实现相同效果的算法参数的唯一性问题。
- Q: Suppose that we found a W such that L=0. Is this W unique?
- No! 2W is also has L=0!
既然不唯一,那么该如何选择 W 呢?
用 Regularization(正则项)!来鼓励模型以某种方式选择更简单的 W! 这也是有效避免过拟合的常用手段之一。如下面的公式!
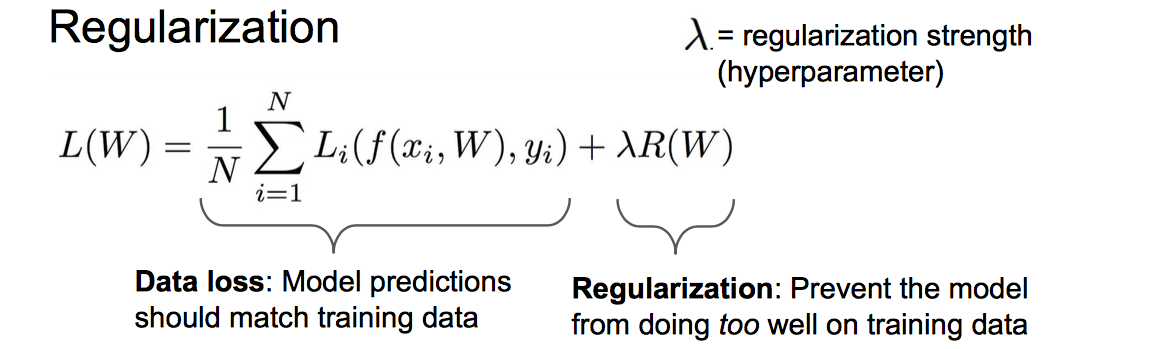
关于正则化,小哥提及到:
大体上有两种思路去避免过拟合:一种是限制你的模型,这个边界在于不要太高的阶数或模型太过复杂;另一种就是加入这种软性惩罚项(正则)。这样一来,模型依然可以逼近复杂模型的效果。如果你想使用这些复杂的模型,你就需要使用惩罚来使用它们的复杂性(complexity)。
小哥又说了一句很有趣的句子,找个小本本抄下来:
This is the picture that many people have in mind.
这是人们至少有的第一反应。
- 关于正则项有如下几个简单例子:
- L2 regularization: $R(W)=\sum_k\sum_lW^2_{k,l}$
- 权重向量 W 的欧式范数 (or the squared norm)。
- L1 regularization: $R(W)=\sum_k\sum_l|W_{k,l}|$
- 权重向量 W 的L1范数;鼓励稀疏化的权重矩阵 W;
- Elastic net (L1+L2): $R(W)=\sum_k\sum_l\beta W^2_{k,l}+|W_{k,l}|$
- Max norm regularization: (penalizing the max norm)
- L2 regularization: $R(W)=\sum_k\sum_lW^2_{k,l}$
- 关于防止过拟合还有更加复杂的手段:
- Dropout
- Batch normalization
- Stochastic depth, fractional pooling, etc
- 话说正则化目的是啥呢?这里总结一下:
- Express preferences over weights
- Make the model simple so it works on test data
- Improve optimization by adding curvature
关于正则化的宏观理念,小哥提到:
你对模型所做的任何种种所谓的惩罚,主要目的是为了减轻模型的复杂度,而不是去试图拟合数据。
- Q: L1/L2 正则化如何度量模型的复杂性?
- L2 regularization likes to “spread out” the weights. 它更加能够传递出数据 x 中不同元素值的影响,这取决于 x 向量的整体情况,而不会取决于 x 向量中某单个元素。它的鲁棒性(robust)也可能更好一些。
- 如果我们采用 L1正则化,其对模型的复杂性具有不同的概念,可能对具有较小的复杂度的模型更加敏感,或者说,它通常更加喜欢稀疏解一些,它倾向于让大部分的 W 元素接近0。
- 对于 L1 度量复杂度的方式,有可能是非零元素的个数;而 L2 更多考虑的是 W 整体的分布,即所有的元素具有较小的复杂性。
- 对于贝叶斯铁杆粉丝来说,L2 正则化可以得到非常好的解释。在 MAP 推理中,是参数向量的高斯先验。
2. Softmax loss (Multinomial Logistic Regression)
这个损失函数和上面 SVM 的一个很大的区别之一就是其输出的得分可以有更多的解释,那就是对于所有类别有相应的概率。
Softmax function: $$ P(Y=k|X=x_i)=\frac{e^{s_k}}{\sum_je^{s_j}},,\ \text{where} , s=f(x_i;W) $$
- 将类别得分指数化以便结果都是正数,接着利用这些指数的和来归一化它们。于是,我们得到了概率分布。
loss function: $$ L_i = -\log P(Y=y_i|X=x_i) $$
Soft loss function 将根据得分结算出来的概率分布与真实的概率分布进行比较,对真实类别概率的对数再取负值: $$ L_i = -\log\Big(\frac{e^{s_{y_i}}}{\sum_je^{s_j}}\Big) $$
由于目标的概率中正确类别的概率是1,其他是0,所以,优化的目标是让预测正确的类别应该具有几乎所有的概率。
除此以外,我们也可以将损失定义为在目标概率分布与计算出的概率分布之间计算 KL 散度(Kullback-Leibler divergence),以比较他们的差异,去做一个最大似然估计 (maximum likelihood estimate):(Q 是 ground truth/correct probs) $$ D_{KL}(P||Q) = \sum_yP(y)\log\frac{P(y)}{Q(y)} $$ 交叉熵(cross entopy): $$ H(P,Q) = H(p) + D_{KL}(P||Q) $$ 具体可以参考下面的几篇文章:
Q: Softmax损失的最大值和最小值?
- 最小值是0(理论值,但永远不会达到这个有限精度的极值),最大值是无穷大。
Q: 若初始化的参数非常的小,呈现较小的均匀分布的值,于是初期所有的得分都近乎为0并且差不多相等,那么合页损失预计会如何?
- log(C),其中C是类别数目.(代码调试策略,健全性检查问题,预期损失函数的值)
- 二分类:log(2) = 0.6931;十分类:log(10) = 2.3
3. Softmax vs. SVM
接下来,我们针对两个已经介绍过的损失函数进行一个简单的对比:
- Q: Suppose I take a datapoint and I jiggle a bit (changing its score slightly). What happens to the loss in both cases?
- SVM 是不会有变化的,因为有一个安全边际的概念;Softmax 会出现变化的。
- SVM 会得到这个数据点若超过阈值要是正确的分类,然后就放弃,不再关心这个数据点;而 Softmax 总是试图不断提高每一个数据点都会越来越好。这是一个有趣的差异。
接下来,我们如何真正发现模型参数 W 使得这个损失函数最小化呢?这就是下面的优化议题了。
4. Optimization
梯度是什么?请翻阅另外一篇原创文章中的小结:跟着梯度走!
为了引入梯度下降,课程硬是先用随机搜索(Random search)参数空间的算法来以示对比。发现精确度才15.5%,倒是比瞎蒙要好点。
接下来,讲解了如果用有限差分法去数值计算梯度 dW 的话是怎样操作的,但是这么搞显然很慢和低效率的。还好我们学的微积分是有用的,因为我们可以直接求出梯度的解析表达式,相当于有另一个关于 dW 的新算法。
于是小哥就开始总结了:
- Numerical gradient:approximate,slow,easy to write
- Analytic gradient:exact,fast,error-prone
值得一提的是,数值梯度法是很有用的调试工具,当你需要查验你写的梯度解析表达式是否正确的时候:
In practice: Always usr analytic gradient, but check implementation with numerical gradient. This is called a gradient check.
一个最 low 版的梯度下降算法怎么写?往下看:
# Vanilla Gradient Descent
while True:
weights_grad = evaluate_gradient(loss_fun, data, weights)
weights += - step_size * weights_grad # perform parameter update
这里的 step_size 叫做学习率(learning rate)。
看个小视频体会一下。。。。(其上鼠标右键点击“显示控制”,然后点击▶️ )
4.1 Stochastic Gradient Descent (SGD)
Recall: $$ L(W) = \frac{1}{N}\sum^N_{i=1}L_i(x_i,y_i,W)+\lambda R(W)\ \nabla_WL(W)=\frac{1}{N}\sum^N_{i=1}\nabla_WL_i(x_i,y_i,W)+\lambda\nabla_WR(W) $$ 但是对整个训练集进行一次梯度计算和参数更新是不现实的,不过我们可以用 a minibatch of examples 。由于这个小批量迭代的样本是随机(Stochastic)采样的,可以把它当做对真实数值期望的一种蒙特卡洛统计。
算法代码可以这样写:
# Vanilla Minibatch Gradient Desent
while True:
data_batch = sample_training_data(data, 256) # sample 256 examples
weights_grad = evaluate_gradient(loss_fun, data_batch, weights)
weights += - step_size * weights_grad
可能觉得这个代码太概念了,没关系下面是一个可交互的网页端供你体会一二:

这对于有直观的感受和直觉是很有帮助的!
5. Aside: Image Features
这里首先谈到的一个重要概念是:特征转换(feature transform)
正确的特征转换,可以计算出所关心问题的正确指标。小哥举了两个例子,我懒得赘述了。。。。
这个精神其实和结构化数据中的特征工程是一回事!
但毕竟是人工特征,可以实现自动化特征提取嘛?
可以!这就是要学的神经网络!深度学习啊!
