Lecture 4. Introduction to Neural Networks

Last updated on Dec 16, 2023 4 min read Tutorial

Table of Contents

CS231n 课程的官方地址：http://cs231n.stanford.edu/index.html
该笔记根据的视频课程版本是 Spring 2017(BiliBili)，PPt 资源版本是 Spring 2018.
另有该 Lecture 3. 扩展讲义资料：
backprop notes [中译版]
linear backprop example
derivatives notes (optional)
Efficient BackProp (optional)
related: 1, 2, 3 (optional)

课程刚一开始，小姐姐的颜值就立马开始吸粉。。。

1. Backpropagation

废话不多说，总结了之前讲的故事后。用计算图总结了线性计算和损失函数后，就立马开始引出本 lecture 中最重要的算法：反向传播算法。

虽然名字是反向传播算法（backpropagation），但其实背后的逻辑是过于简单的：链式法则嘛。此处不再赘述，欢迎直接阅读：一段关于神经网络的故事。

Q：为什么不用微积分理论直接计算参数的梯度呢？
- 当面对复杂表达式的时候，将其分解为一些计算节点，可以非常简单的计算得出梯度。
Note：关于节点们的部分组合可以很好的实现更简洁更快速的梯度计算图表达。比如说，sigmoid function $\sigma(x)=\frac{1}{1+e^{-x}}$ 就有： $$ \frac{d\sigma(x)}{dx}=\frac{e^{-x}}{(1+e^{-x})^2}=\Big(\frac{1+e^{-x}-1}{1+e^{-x}}\Big)\Big(\frac{1}{1+e^{-x}}\Big)=(1-\sigma(x))\sigma(x) $$

经过几个小例子的考验，我们似乎可以总结出规律了：

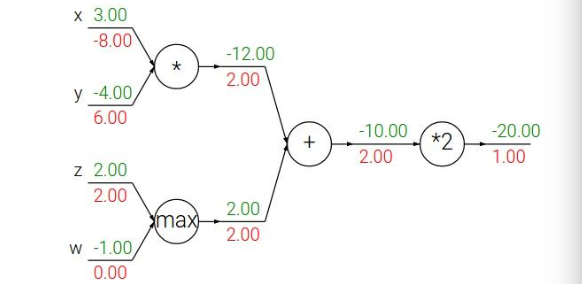
Patterns in backward flow
- add gate: gradient distributor. 梯度分布器：反向分发和传递相同的梯度值
- max gate: gradient router. 梯度路由器：反向传递在前向中较大值方向的梯度值
- mul gate: gradient switcher. 梯度转换/缩放器：根据另一个分支的值对梯度进行缩放
这时候有个学生提了一个问题：这梯度数字经过如此一番计算后，那如何更新参数呢？
- 其实，我的理解是：上面👆图像中最左侧得到的不同的红色梯度数字就是暗示了这些参数究竟对最后的损失值在动态的迭代更新中是怎样的静态变化。有的绝对值数字大，不就是说丫的参数应该多给点力，绝对值数字小的就是说这个参数可以先“按兵不动”，数字的符号自然也就直接决定了该参数对损失值变化的方向。那么所谓的参数更新就是最优化问题了，看你怎么利用这个梯度数字了。

数字的前向/反向传播说完后，就要推广到矢量的前向/反向传播了。

其实不可怕，不就是对称的雅克比矩阵嘛~ （Wiki）

Always check: The gradient with respect to a variable should have the same shape as the variable.

后面就真没啥内容了。可以简单的总结为：需要自己动笔琢磨，自己动手代码才能彻底理解。

还有扩展资料是非常干的~ ，你懂滴！

2. Neural Networks

课程刚一开始就强调：without the brain stuff！简单地说，就是不要跟我扯什么生物神经元啥的~ 这个概念早已与之分道扬镳~

随后的两层神经网络讲的有些稀里糊涂，视频里居然没有说清楚非线性就是 $\max$ 函数，不如看我自己写的这一部分（一个神经元的本事）。又是那句话，扯半天概念和流程图，都不如直接看代码来的实在：

import numpy as np
from numpy.random import randn

N, D_in, H, D_out = 64, 1000, 100, 10
x, y = randn(N, D_in), randn(N, D_out)
w1, w2 = randn(D_in, H), randn(H, D_out)

for t in range(2000):
    h = 1 / (1 + np.exp(-x.dot(w1)))
    y_pred = h.dot(w2)
    loss = np.square(y_pred - y).sum()
    print(t, loss)
    
    grad_y_pred = 2.0 * (y_pred - y)
    grad_w2 = h.T.dot(grad_y_pred)
    grad_d = grad_y_pred.dot(w2.T)
    grad_w1 = x.T.dot(grad_h * h * (1 - h))
    
    w1 -= 1e-4 * grad_w1
    w2 -= 1e-4 * grad_w2

上面是一个两层神经网络，有一个单隐层的结构。作业就是以此作为灵感，也写一个两层全连接的神经网络。

接下来的内容（除了神经元类比），就开始真正有些干货出来了，主要是这个图：

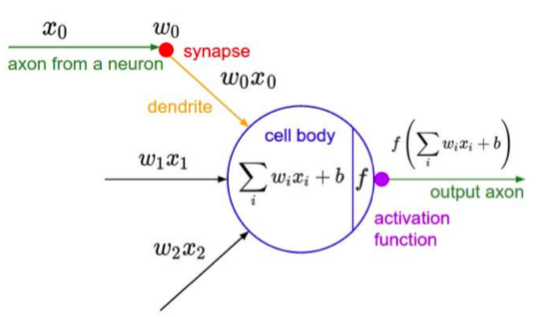
这就是一个神经元的本事。既有线性变换，也有非线性加持。差不多是最一般意义的基础计算单元。代码可以如下表示：

class Neuron:
    # ...
    def neuron_tick(input):
        """ assume inputs and weights are 1-D numpy arrays and bias is a number"""
        cell_body_sum = np.sum(inputs * self.weights) + self.bias
        firing_rate = 1.0 / (1.0 + math.exp(-cell_body_sum)) # sigmoid activation function
        return firing_rate

很快地，小姐姐又开始警告不要随便和生物学扯上关系！

Be very careful with your brain analogies!

Biological Neurons：
- Many different types
- Dendrites can perform complex non-linear computations
- Synapses are not a singal weight but a complex non-linear dynamical system
- Rate code may not be adequate

2.1 Activation functions

视频里列出了一波常见的激活函数，但是居然没有细讲，直接飞过去了：

然后，强调了不同层的全连接神经网络的叫法：

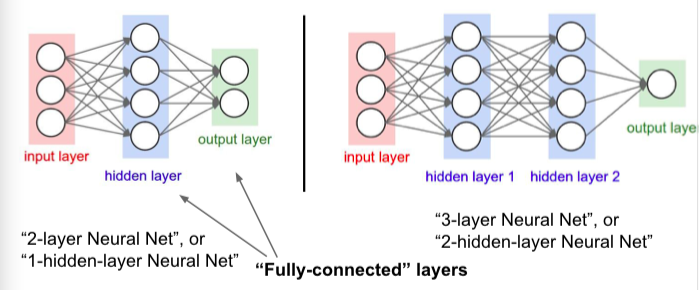
最后，又说其实我们刚刚代码是针对一个神经元的计算，其实我们可以推广到一层神经元的操作。比如上图右面的3层神经网络（两个隐藏层），利用矩阵乘法，可以这么写代码：

# forward-pass of a 3-layer neural network:
f = lambda x: 1.0/(1.0 + np.exp(-x)) # activation function (use sigmoid)
x = np.random.randn(3, 1) # random input vector of three numbers (3x1)
h1 = f(np.dot(W1, x) + b1) # calculate first hidden layer activations (4x1)
h2 = f(np.dot(W2, h1) + b2) # calculate second hidden layer activations (4x1)
out = np.dot(W3, h2) + b3

再然后。。。这节课就结束啦！！。。。

CS231n Python Deep Learning Machine Learning

Lecture 4. Introduction to Neural Networks

1. Backpropagation

2. Neural Networks

2.1 Activation functions

Related