Lecture 5. Convolutional Neural Networks

Last updated on Dec 16, 2023 4 min read Tutorial
Project
Table of Contents

CS231n 课程的官方地址：http://cs231n.stanford.edu/index.html

该笔记根据的视频课程版本是 Spring 2017(BiliBili)，PPt 资源版本是 Spring 2018.

另有该 Lecture 5. 扩展讲义资料：

1. A bit of history…

这需要追溯到 1957年。。。 Frank RosenBlatt 发明了第一代感知机器，首次实现了所谓的感知器算法。它在思想上跟得到评分函数的过程类似。也有所谓的参数更新规则，看似和反向传播算法很像，但此时 BP 还没有被发明出来。。。

在 1960 年，Widrow 和 Hoff 发明了 Adaline 和 Madaline。这是首次尝试把线性层叠加整合为多层感知器网络。现在好像与神经网络的层的设计比较接近，但反向传播或者其他的训练方法仍未出现。

到 1986 年，Rumelhart 才首次提出了反向传播算法。从这里开始我们有了最核心的训练方法。

不过再很长一段时间内，我们仍然无法训练超大型神经网络。所谓的神经网络领域曾经常年无人问津，并不用说大规模应用了。但在 2000 年左右，事情开始有了变化。

在 2006 年，Geoff. Hinton 与 Ruslan Salakhutdinov 合作的一篇论文，表明深度神经网络不仅可以训练并且可以高效训练。这仍然不是神经网络现在的样子。此时的网络需要谨慎的初始化才能运行反向传播。他们的方法就是先经过一个预训练阶段，对每一个隐层使用受限玻尔兹曼机（restricted Boltzmann machine）来建模。这样通过迭代训练每一层可以得到一些初始化权重，得到所有的隐层之后，以此来初始化一个完整的神经网络。然后反向传播，微调参数。

实际上，直到 2012 年。神经网络才第一次取得了惊人的成果。深度神经网络的狂潮由此爆发。第一个被攻破的领域是语音识别，Geoff. Hinton 组利用深度神经网络进行声学建模和语音识别。然后是图像识别，在 2012 年，Geoff. Hinton 同一个实验室的 Alex Krizhevsky 发表了里程碑式的[论文](../paper_summary/ImageNet Classification with Deep Convolutional Neural Networks.html)，首次让卷积神经网络的框架在 ImageNet 分类大赛中取得了惊人的成绩。CNN 树立了 ImageNet 图像分类任务的标杆，并且大幅降低了误差。此后，卷积神经网络开始得到广泛的应用。

接下来，扯的是视觉任务的历史。。。和 Lecture.1 基本差不多。

远的不说，直接从 1998 年说起。Yann LeCun 首次简单展示了第一个实例：应用反向传播和基于梯度的学习方法，来训练卷积神经网络。这对文档识别非常有效，尤其对邮政编码识别效果极好。因此这些方法在邮政服务中被广泛用于邮政编码识别。然而它并不能扩展到更具有挑战、更复杂的数据。数字非常容易识别，但识别也是有局限性的。

于是在 2012 年，Alex Krizhevsky 提出了一种现代化的卷积神经网络。他提出的网络，我们一般称为 [AlexNet](../paper_summary/ImageNet Classification with Deep Convolutional Neural Networks.html)。但他的网络和 Yann LeCun 提出的卷积神经网络相比，看上去并没有多大差异。它们只是扩展的更大更深。更重要的一部分是它们可以充分利用大量数据可得到的图像（ImageNet 数据集）。同时也充分发挥了 GPU 并行计算能力的优势。

现在，ConvNets 已经被广泛应用。

接下来，小姐姐介绍了各种各样啊的应用，只有一个星系分类和我的领域略有相关：https://arxiv.org/pdf/1503.07077.pdf

2. Convolutional Neural Networks

(First without the brain stuff)

我们从函数的角度来讨论卷积神经网络。（我这里省略掉了卷积的操作细节）

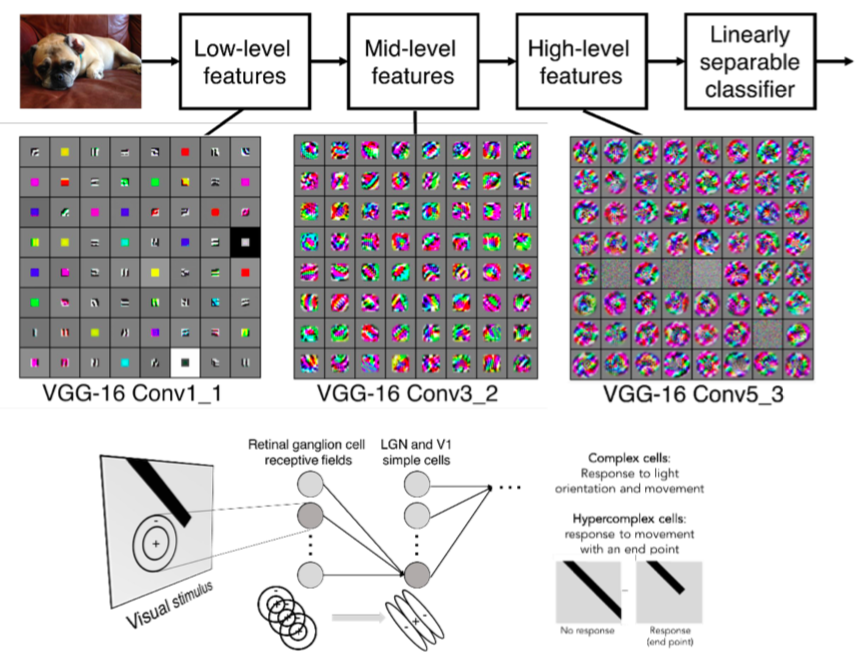
  • 前面几层的卷积核一般代表了一些低阶的图像特征，比如说一些边缘特征。之后几层的特征会更加的复杂，它的内容看起来可能更加丰富。对于那些高阶的特征，可以获得一些比斑点之类的更加丰富的内容。

  • 信号处理中的二维卷积： $$ f[x,y]*g[x,y]=\sum^\infty_{n_1=-\infty}\sum^\infty_{n_2=-\infty}f[n_1,n_2]\cdot g[x-n_1,y-n_2] $$ （elementwise multiplication and sum of a filter and the signal）

巴拉巴拉。。。说了很多，总之就是下面👇总结的好东西：（其实还不全~）

2.1 Summary. To summarize, the Conv Layer:

  • Accepts a volume of size $W_1\times H_1\times D_1$
  • Requires four hyperparameters:
    • Number of filters $K$. (powers of 2, e.g. 32, 64, 128, 512)
    • their spatial extent $F$.
    • the stride $S$.
    • the amount of zero padding $P$.
  • Produces a volume of size $W_2\times H_2\times D_2$ where:
    • $W_2=(W_1-F+2P)/2+1$
    • $H_2=(H_1-F+2P)/2+1$ (i.e. width and height are computed equally by symmetry)
    • $D_2=K$
  • With parameter sharing, it introduces $F\cdot F\cdot D_1$ weights per filter, for a total of $(F\cdot F\cdot D_1)\cdot K$ weights and $K$ biases.
  • In the output volume, the $d$-th depth slice (of size $W_2\times H_2$) is the result of performing a valid convolution of the $d$-th filter over the input volume with a stride of $S$, and then offset by $d$-th bias.

神经元角度的解读就略过了，没啥意思。。。唯独一个感受野（receptive field） 这个概念是很重要的，但是这个讲义还没讲清楚讲全。

对于池化层，我们也可以总结一下：

2.2 Summary. To summarize, the Pooling Layer:

  • Accepts a volume of size $W_1\times H_1\times D_1$
  • Requires three hyperparameters: (Common settings: $F=2,S=2$ or $F=3, S=3$)
    • their spatial extent $F$,
    • the stride $S$,
  • Produces a volume of size $W_2\times H_2\times D_2$ where:
    • $W_2=(W_1-F)/S+1$
    • $H_2=(H_1-F)/S+1$
    • $D_2=D_1$
  • Introduces zero parameters since it computes a fixed function of the input
  • Note that it is not common to use zero-padding for Pooling layers

2.3 Demo

最最后，show 出了一个 demo 可以在 CIFAR-10数据集上观察训练过程以及训练后的可视化效果。

https://cs.stanford.edu/people/karpathy/convnetjs/demo/cifar10.html

CS231n Python Deep Learning Machine Learning
Next
Previous

Related