CS231n课程讲义翻译:图像分类
自注:此文是在转载的基础上,通过网络搜集其他相关学习资料,再结合自己理解下,填充并注释了更多的细节和内容,以此详尽的文本资料代替各种视频课程等资料,方便自己回头翻查。
转载请注明本文出处和原译文出处。
(个人填充的内容包括:下划线、注明“自注”)
译者注:本文智能单元首发,译自斯坦福CS231n课程笔记image classification notes,由课程教师Andrej Karpathy授权进行翻译。本篇教程由杜客翻译完成。ShiqingFan对译文进行了仔细校对,提出了大量修改建议,态度严谨,帮助甚多。巩子嘉对几处术语使用和翻译优化也提出了很好的建议。张欣等亦有帮助。
这是一篇介绍性教程,面向非计算机视觉领域的同学。教程将向同学们介绍图像分类问题和数据驱动方法。下面是内容列表:
- 图像分类、数据驱动方法和流程
- Nearest Neighbor分类器
- k-Nearest Neighbor
- 验证集、交叉验证集和超参数调参
- Nearest Neighbor的优劣
- 小结
- 小结:应用kNN实践
- 拓展阅读
- 作业:k-Nearest Neighbor (kNN)
1. 图像分类
目标:这一节我们将介绍图像分类问题。所谓图像分类问题,就是已有固定的分类标签集合,然后对于输入的图像,从分类标签集合中找出一个分类标签,最后把分类标签分配给该输入图像。虽然看起来挺简单的,但这可是计算机视觉领域的核心问题之一,并且有着各种各样的实际应用。在后面的课程中,我们可以看到计算机视觉领域中很多看似不同的问题(比如物体检测和分割),都可以被归结为图像分类问题。
例子:以下图为例,图像分类模型读取该图片,并生成该图片属于集合 {cat, dog, hat, mug}中各个标签的概率。需要注意的是,对于计算机来说,图像是一个由数字组成的巨大的3维数组。在这个例子中,猫的图像大小是宽248像素,高400像素,有3个颜色通道,分别是红、绿和蓝(简称RGB)。如此,该图像就包含了248X400X3=297600个数字,每个数字都是在范围0-255之间的整型,其中0表示全黑,255表示全白。我们的任务就是把这些上百万的数字变成一个简单的标签,比如“猫”。
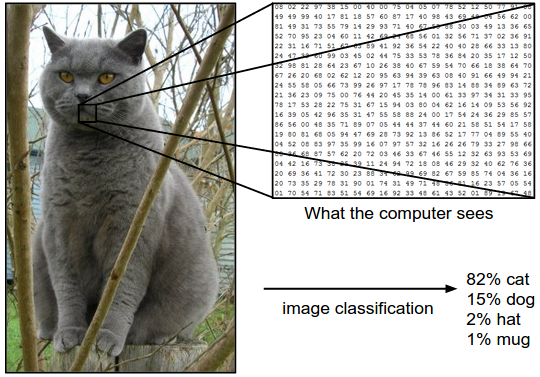
图像分类的任务,就是对于一个给定的图像,预测它属于的那个分类标签(或者给出属于一系列不同标签的可能性)。图像是3维数组,数组元素是取值范围从0到255的整数。数组的尺寸是宽度x高度x3,其中这个3代表的是红、绿和蓝3个颜色通道。
困难和挑战:对于人来说,识别出一个像“猫”一样视觉概念是简单至极的,然而从计算机视觉算法的角度来看就值得深思了。我们在下面列举了计算机视觉算法在图像识别方面遇到的一些困难,要记住图像是以3维数组来表示的,数组中的元素是亮度值。
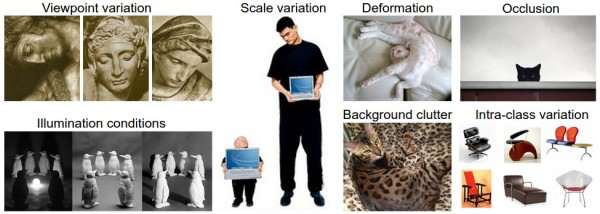
- 视角变化(Viewpoint variation):同一个物体,摄像机可以从多个角度来展现。
- 大小变化(Scale variation):物体可视的大小通常是会变化的(不仅是在图片中,在真实世界中大小也是变化的)。
- 形变(Deformation):很多东西的形状并非一成不变,会有很大变化。
- 遮挡(Occlusion):目标物体可能被挡住。有时候只有物体的一小部分(可以小到几个像素)是可见的。
- 光照条件(Illumination conditions):在像素层面上,光照的影响非常大。
- 背景干扰(Background clutter):物体可能混入背景之中,使之难以被辨认。
- 类内差异(Intra-class variation):一类物体的个体之间的外形差异很大,比如椅子。这一类物体有许多不同的对象,每个都有自己的外形。
面对以上所有变化及其组合,好的图像分类模型能够在维持分类结论稳定的同时,保持对类间差异足够敏感。
数据驱动方法:如何写一个图像分类的算法呢?这和写个排序算法可是大不一样。怎么写一个从图像中认出猫的算法?搞不清楚。因此,与其在代码中直接写明各类物体到底看起来是什么样的,倒不如说我们采取的方法和教小孩儿看图识物类似:给计算机很多数据,然后实现学习算法,让计算机学习到每个类的外形。这种方法,就是数据驱动方法。既然该方法的第一步就是收集已经做好分类标注的图片来作为训练集,那么下面就看看数据库到底长什么样:
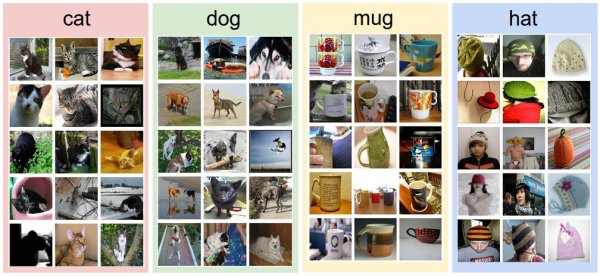
一个有4个视觉分类的训练集。在实际中,我们可能有上千的分类,每个分类都有成千上万的图像。
图像分类流程。在课程视频中已经学习过,图像分类就是输入一个元素为像素值的数组,然后给它分配一个分类标签。完整流程如下:
- 输入:输入是包含N个图像的集合,每个图像的标签是K种分类标签中的一种。这个集合称为训练集。
- 学习:这一步的任务是使用训练集来学习每个类到底长什么样。一般该步骤叫做训练分类器或者学习一个模型。
- 评价:让分类器来预测它未曾见过的图像的分类标签,并以此来评价分类器的质量。我们会把分类器预测的标签和图像真正的分类标签对比。毫无疑问,分类器预测的分类标签和图像真正的分类标签如果一致,那就是好事,这样的情况越多越好。
2. Nearest Neighbor分类器
作为课程介绍的第一个方法,我们来实现一个Nearest Neighbor分类器。虽然这个分类器和卷积神经网络没有任何关系,实际中也极少使用,但通过实现它,可以让读者对于解决图像分类问题的方法有个基本的认识。
图像分类数据集:CIFAR-10。一个非常流行的图像分类数据集是CIFAR-10。这个数据集包含了60000张32X32的小图像。每张图像都有10种分类标签中的一种。这60000张图像被分为包含50000张图像的训练集和包含10000张图像的测试集。在下图中你可以看见10个类的10张随机图片。

左边:从CIFAR-10数据库来的样本图像。右边:第一列是测试图像,然后第一列的每个测试图像右边是使用Nearest Neighbor算法,根据像素差异,从训练集中选出的10张最类似的图片。
假设现在我们有CIFAR-10的50000张图片(每种分类5000张)作为训练集,我们希望将余下的10000作为测试集并给他们打上标签。Nearest Neighbor算法将会拿着测试图片和训练集中每一张图片去比较,然后将它认为最相似的那个训练集图片的标签赋给这张测试图片。上面右边的图片就展示了这样的结果。请注意上面10个分类中,只有3个是准确的。比如第8行中,马头被分类为一个红色的跑车,原因在于红色跑车的黑色背景非常强烈,所以这匹马就被错误分类为跑车了。
那么具体如何比较两张图片呢?在本例中,就是比较32x32x3的像素块。最简单的方法就是逐个像素比较,最后将差异值全部加起来。换句话说,就是将两张图片先转化为两个向量$I_1$和$I_2$,然后计算他们的L1距离: $$ d_1(I_1,I_2)=\sum_p|I^p_1-I^p_2| $$ 这里的求和是针对所有的像素。下面是整个比较流程的图例:
(自注:每个对应像素之差的结果全部取和——所谓L1距离)
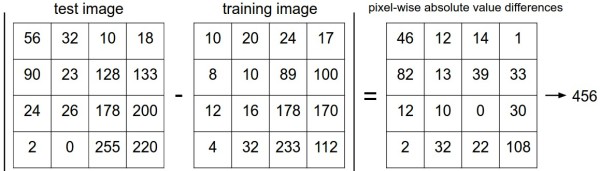
以图片中的一个颜色通道为例来进行说明。两张图片使用L1距离来进行比较。逐个像素求差值,然后将所有差值加起来得到一个数值。如果两张图片一模一样,那么L1距离为0,但是如果两张图片很是不同,那L1值将会非常大。
下面,让我们看看如何用代码来实现这个分类器。首先,我们将CIFAR-10的数据加载到内存中,并分成4个数组:训练数据和标签,测试数据和标签。在下面的代码中,Xtr(大小是50000x32x32x3)存有训练集中所有的图像,Ytr是对应的长度为50000的1维数组,存有图像对应的分类标签(从0到9):
Xtr, Ytr, Xte, Yte = load_CIFAR10('data/cifar10/') # a magic function we provide
# flatten out all images to be one-dimensional
Xtr_rows = Xtr.reshape(Xtr.shape[0], 32 * 32 * 3) # Xtr_rows becomes 50000 x 3072
Xte_rows = Xte.reshape(Xte.shape[0], 32 * 32 * 3) # Xte_rows becomes 10000 x 3072
(自注:训练集中有50000张图片,每个图片reshape成为了一条一维的数组,共3072个元素。)
现在我们得到所有的图像数据,并且把他们拉长成为行向量了。接下来展示如何训练并评价一个分类器:
nn = NearestNeighbor() # create a Nearest Neighbor classifier class
nn.train(Xtr_rows, Ytr) # train the classifier on the training images and labels
Yte_predict = nn.predict(Xte_rows) # predict labels on the test images
# and now print the classification accuracy, which is the average number
# of examples that are correctly predicted (i.e. label matches)
print 'accuracy: %f' % ( np.mean(Yte_predict == Yte) ) # python2.x
作为评价标准,我们常常使用准确率,它描述了我们预测正确的得分。请注意以后我们实现的所有分类器都需要有这个API:train(X, y) 函数。该函数使用训练集的数据和标签来进行训练。从其内部来看,类应该实现一些关于标签和标签如何被预测的模型。这里还有个 predict(X) 函数,它的作用是预测输入的新数据的分类标签。现在还没介绍分类器的实现,下面就是使用L1距离的Nearest Neighbor分类器的实现套路:
import numpy as np
class NearestNeighbor(object):
def __init__(self):
pass
def train(self, X, y):
"""
这个地方的训练其实就是把所有的已有图片读取进来 -_-||
"""
""" X is N x D where each row is an example. Y is 1-dimension of size N """
# the nearest neighbor classifier simply remembers all the training data
self.Xtr = X
self.ytr = y
def predict(self, X):
"""
所谓的预测过程其实就是扫描所有训练集中的图片,计算距离,取最小的距离对应图片的类目
"""
""" X is N x D where each row is an example we wish to predict label for """
num_test = X.shape[0]
# 这里要保证维度一致!
# lets make sure that the output type matches the input type
Ypred = np.zeros(num_test, dtype = self.ytr.dtype) # 一维元素都是0的array
# 把训练集扫一遍 -_-||
# loop over all test rows
for i in xrange(num_test):
# 注意这里的xrange仅适用于python2.x,range适用于python3.x
# find the nearest training image to the i'th test image
# using the L1 distance (sum of absolute value differences)
# 对训练集中每一张图片都与指定的一张测试图片,在对应元素位置上做差,
# 然后分别以每张图片为单位求和。
distances = np.sum(np.abs(self.Xtr - X[i,:]), axis = 1) # 一个5000元素的list
# 取最小distance图片的下标:
min_index = np.argmin(distances) # get the index with smallest distance
Ypred[i] = self.ytr[min_index] # predict the label of the nearest example
return Ypred
如果你用这段代码跑CIFAR-10,你会发现准确率能达到38.6%。这比随机猜测的10%要好,但是比人类识别的水平(据研究推测是94%)和卷积神经网络能达到的95%还是差多了。点击查看基于CIFAR-10数据的Kaggle算法竞赛排行榜。
距离选择:计算向量间的距离有很多种方法,另一个常用的方法是L2距离,从几何学的角度,可以理解为它在计算两个向量间的欧式距离。L2距离的公式如下: $$ d_2(I_1,I_2)=\sqrt{\sum_p(I^P_1-I^p_2)^2} $$ 换句话说,我们依旧是在计算像素间的差值,只是先求其平方,然后把这些平方全部加起来,最后对这个和开方。在Numpy中,我们只需要替换上面代码中的1行代码就行:
distances = np.sqrt(np.sum(np.square(self.Xtr - X[i,:]), axis = 1))
注意在这里使用了np.sqrt,但是在实际中可能不用。因为求平方根函数是一个单调函数,它对不同距离的绝对值求平方根虽然改变了数值大小,但依然保持了不同距离大小的顺序。所以用不用它,都能够对像素差异的大小进行正确比较。如果你在CIFAR-10上面跑这个模型,正确率是35.4%,比刚才低了一点。
L1和L2比较。比较这两个度量方式是挺有意思的。在面对两个向量之间的差异时,L2比L1更加不能容忍这些差异。也就是说,相对于1个巨大的差异,L2距离更倾向于接受多个中等程度的差异。L1和L2都是在p-norm常用的特殊形式。
(自注:更多的距离准则可以参见scipy相关计算页面.)
3. k-Nearest Neighbor分类器
你可能注意到了,为什么只用最相似的1张图片的标签来作为测试图像的标签呢?这不是很奇怪吗!是的,使用k-Nearest Neighbor分类器就能做得更好。它的思想很简单:与其只找最相近的那1个图片的标签,我们找最相似的k个图片的标签,然后让他们针对测试图片进行投票,最后把票数最高的标签作为对测试图片的预测。所以当k=1的时候,k-Nearest Neighbor分类器就是Nearest Neighbor分类器。从直观感受上就可以看到,更高的k值可以让分类的效果更平滑,使得分类器对于异常值更有抵抗力。
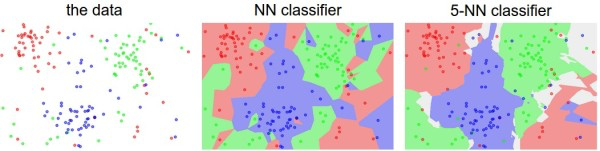
上面示例展示了Nearest Neighbor分类器和5-Nearest Neighbor分类器的区别。例子使用了2维的点来表示,分成3类(红、蓝和绿)。不同颜色区域代表的是使用L2距离的分类器的决策边界。白色的区域是分类模糊的例子(即图像与两个以上的分类标签绑定)。需要注意的是,在NN分类器中,异常的数据点(比如:在蓝色区域中的绿点)制造出一个不正确预测的孤岛。5-NN分类器将这些不规则都平滑了,使得它针对测试数据的 泛化(generalization)能力更好(例子中未展示)。注意,5-NN中也存在一些灰色区域,这些区域是因为近邻标签的最高票数相同导致的(比如:2个邻居是红色,2个邻居是蓝色,还有1个是绿色)。
在实际中,大多使用k-NN分类器。但是k值如何确定呢?接下来就讨论这个问题。
4. 用于超参数调优的验证集
k-NN分类器需要设定k值,那么选择哪个k值最合适的呢?我们可以选择不同的距离函数,比如L1范数和L2范数等,那么选哪个好?还有不少选择我们甚至连考虑都没有考虑到(比如:点积)。所有这些选择,被称为超参数(hyperparameter)。在基于数据进行学习的机器学习算法设计中,超参数是很常见的。一般说来,这些超参数具体怎么设置或取值并不是显而易见的。
你可能会建议尝试不同的值,看哪个值表现最好就选哪个。好主意!我们就是这么做的,但这样做的时候要非常细心。特别注意:决不能使用测试集来进行调优。当你在设计机器学习算法的时候,应该把测试集看做非常珍贵的资源,不到最后一步,绝不使用它。如果你使用测试集来调优,而且算法看起来效果不错,那么真正的危险在于:算法实际部署后,性能可能会远低于预期。这种情况,称之为算法对测试集过拟合。从另一个角度来说,如果使用测试集来调优,实际上就是把测试集当做训练集,由测试集训练出来的算法再跑测试集,自然性能看起来会很好。这其实是过于乐观了,实际部署起来效果就会差很多。所以,最终测试的时候再使用测试集,可以很好地近似度量你所设计的分类器的泛化性能(在接下来的课程中会有很多关于泛化性能的讨论)。
测试数据集只使用一次,即在训练完成后评价最终的模型时使用。
好在我们有不用测试集调优的方法。其思路是:从训练集中取出一部分数据用来调优,我们称之为验证集(validation set)。以CIFAR-10为例,我们可以用49000个图像作为训练集,用1000个图像作为验证集。验证集其实就是作为假的测试集来调优。下面就是代码:
# 假定已经有Xtr_rows, Ytr, Xte_rows, Yte了,其中Xtr_rows为50000*3072 矩阵
# assume we have Xtr_rows, Ytr, Xte_rows, Yte as before
# recall Xtr_rows is 50,000 x 3072 matrix
Xval_rows = Xtr_rows[:1000, :] # take first 1000 for validation 构建前1000个图为交叉验证集
Yval = Ytr[:1000]
Xtr_rows = Xtr_rows[1000:, :] # keep last 49,000 for train 保留其余49000个图为训练集
Ytr = Ytr[1000:]
# 设置一些k值,用于试验
# find hyperparameters that work best on the validation set
validation_accuracies = []
for k in [1, 3, 5, 10, 20, 50, 100]:
# 初始化对象
# use a particular value of k and evaluation on validation data
nn = NearestNeighbor()
nn.train(Xtr_rows, Ytr)
# 修改一下predict函数,接受 k 作为参数
# here we assume a modified NearestNeighbor class that can take a k as input
Yval_predict = nn.predict(Xval_rows, k = k)
acc = np.mean(Yval_predict == Yval)
print 'accuracy: %f' % (acc,)
# 输出结果
# keep track of what works on the validation set
validation_accuracies.append((k, acc)) # 元组形式append在列表里
程序结束后,我们会作图分析出哪个k值表现最好,然后用这个k值来跑真正的测试集,并作出对算法的评价。
把训练集分成训练集和验证集。使用验证集来对所有超参数调优。最后只在测试集上跑一次并报告结果。
交叉验证。有时候,训练集数量较小(因此验证集的数量更小),人们会使用一种被称为交叉验证的方法,这种方法更加复杂些。还是用刚才的例子,如果是交叉验证集,我们就不是取1000个图像,而是将训练集平均分成5份,其中4份用来训练,1份用来验证。然后我们循环着取其中4份来训练,其中1份来验证,最后取所有5次验证结果的平均值作为算法验证结果。
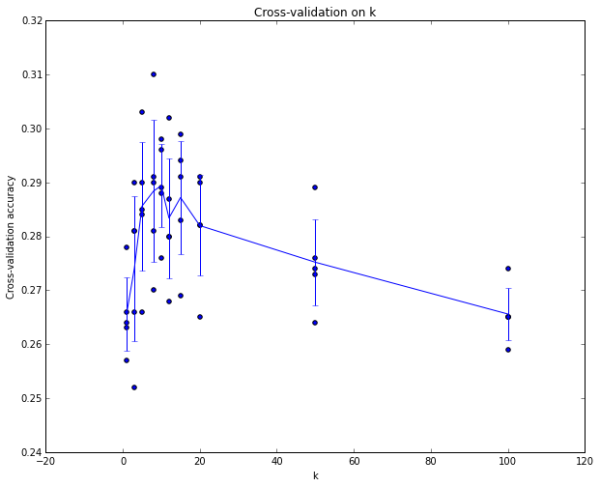
这就是5份交叉验证对k值调优的例子。针对每个k值,得到5个准确率结果,取其平均值,然后对不同k值的平均表现画线连接。本例中,当k=7的时算法表现最好(对应图中的准确率峰值)。如果我们将训练集分成更多份数,直线一般会更加平滑(噪音更少)。
实际应用。在实际情况下,人们不是很喜欢用交叉验证,主要是因为它会耗费较多的计算资源。一般直接把训练集按照50%-90%的比例分成训练集和验证集。但这也是根据具体情况来定的:如果超参数数量多,你可能就想用更大的验证集,而验证集的数量不够,那么最好还是用交叉验证吧。至于分成几份比较好,一般都是分成3、5和10份。

常用的数据分割模式。给出训练集和测试集后,训练集一般会被均分。这里是分成5份。前面4份用来训练,黄色那份用作验证集调优。如果采取交叉验证,那就各份轮流作为验证集。最后模型训练完毕,超参数都定好了,让模型跑一次(而且只跑一次)测试集,以此测试结果评价算法。
5. Nearest Neighbor分类器的优劣
现在对Nearest Neighbor分类器的优缺点进行思考。首先,Nearest Neighbor分类器易于理解,实现简单。其次,算法的训练不需要花时间,因为其训练过程只是将训练集数据存储起来。然而测试要花费大量时间计算,因为每个测试图像需要和所有存储的训练图像进行比较,这显然是一个缺点。在实际应用中,我们关注测试效率远远高于训练效率。其实,我们后续要学习的卷积神经网络在这个权衡上走到了另一个极端:虽然训练花费很多时间,但是一旦训练完成,对新的测试数据进行分类非常快。这样的模式就符合实际使用需求。
Nearest Neighbor分类器的计算复杂度研究是一个活跃的研究领域,若干 Approximate Nearest Neighbor (ANN)算法和库的使用可以提升Nearest Neighbor分类器在数据上的计算速度(比如:FLANN)。这些算法可以在准确率和时空复杂度之间进行权衡,并通常依赖一个预处理/索引过程,这个过程中一般包含kd树的创建和k-means算法的运用。
Nearest Neighbor分类器在某些特定情况(比如数据维度较低)下,可能是不错的选择。但是在实际的图像分类工作中,很少使用。因为图像都是高维度数据(他们通常包含很多像素),而高维度向量之间的距离通常是反直觉的。下面的图片展示了基于像素的相似和基于感官的相似是有很大不同的:

在高维度数据上,基于像素的的距离和感官上的非常不同。上图中,右边3张图片和左边第1张原始图片的L2距离是一样的。很显然,基于像素比较的相似和感官上以及语义上的相似是不同的。
这里还有个视觉化证据,可以证明使用像素差异来比较图像是不够的。这是一个叫做t-SNE的可视化技术,它将CIFAR-10中的图片按照二维方式排布,这样能很好展示图片之间的像素差异值。在这张图片中,排列相邻的图片L2距离就小。

上图使用t-SNE的可视化技术将CIFAR-10的图片进行了二维排列。排列相近的图片L2距离小。可以看出,图片的排列是被背景主导而不是图片语义内容本身主导。
具体说来,这些图片的排布更像是一种颜色分布函数,或者说是基于背景的,而不是图片的语义主体。比如,狗的图片可能和青蛙的图片非常接近,这是因为两张图片都是白色背景。从理想效果上来说,我们肯定是希望同类的图片能够聚集在一起,而不被背景或其他不相关因素干扰。为了达到这个目的,我们不能止步于原始像素比较,得继续前进。
6. 小结
简要说来:
- 介绍了图像分类问题。在该问题中,给出一个由被标注了分类标签的图像组成的集合,要求算法能预测没有标签的图像的分类标签,并根据算法预测准确率进行评价。
- 介绍了一个简单的图像分类器:最近邻分类器(Nearest Neighbor classifier)。分类器中存在不同的超参数(比如k值或距离类型的选取),要想选取好的超参数不是一件轻而易举的事。
- 选取超参数的正确方法是:将原始训练集分为训练集和验证集,我们在验证集上尝试不同的超参数,最后保留表现最好那个。
- 如果训练数据量不够,使用交叉验证方法,它能帮助我们在选取最优超参数的时候减少噪音。
- 一旦找到最优的超参数,就让算法以该参数在测试集跑且只跑一次,并根据测试结果评价算法。
- 最近邻分类器能够在CIFAR-10上得到将近40%的准确率。该算法简单易实现,但需要存储所有训练数据,并且在测试的时候过于耗费计算能力。
- 最后,我们知道了仅仅使用L1和L2范数来进行像素比较是不够的,图像更多的是按照背景和颜色被分类,而不是语义主体分身。
在接下来的课程中,我们将专注于解决这些问题和挑战,并最终能够得到超过90%准确率的解决方案。该方案能够在完成学习就丢掉训练集,并在一毫秒之内就完成一张图片的分类。
7. 小结:实际应用k-NN
如果你希望将k-NN分类器用到实处(最好别用到图像上,若是仅仅作为练手还可以接受),那么可以按照以下流程:
- 预处理你的数据:对你数据中的特征进行归一化(normalize),让其具有零平均值(zero mean)和单位方差(unit variance)。在后面的小节我们会讨论这些细节。本小节不讨论,是因为图像中的像素都是同质的,不会表现出较大的差异分布,也就不需要标准化处理了。
- 如果数据是高维数据,考虑使用降维方法,比如PCA(wiki ref, CS229ref, blog ref)或随机投影。
- 将数据随机分入训练集和验证集。按照一般规律,70%-90% 数据作为训练集。这个比例根据算法中有多少超参数,以及这些超参数对于算法的预期影响来决定。如果需要预测的超参数很多,那么就应该使用更大的验证集来有效地估计它们。如果担心验证集数量不够,那么就尝试交叉验证方法。如果计算资源足够,使用交叉验证总是更加安全的(份数越多,效果越好,也更耗费计算资源)。
- 在验证集上调优,尝试足够多的k值,尝试L1和L2两种范数计算方式。
- 如果分类器跑得太慢,尝试使用Approximate Nearest Neighbor库(比如FLANN)来加速这个过程,其代价是降低一些准确率。
- 对最优的超参数做记录。记录最优参数后,是否应该让使用最优参数的算法在完整的训练集上运行并再次训练呢?因为如果把验证集重新放回到训练集中(自然训练集的数据量就又变大了),有可能最优参数又会有所变化。在实践中,不要这样做。千万不要在最终的分类器中使用验证集数据,这样做会破坏对于最优参数的估计。直接使用测试集来测试用最优参数设置好的最优模型,得到测试集数据的分类准确率,并以此作为你的kNN分类器在该数据上的性能表现。
8. 拓展阅读
下面是一些你可能感兴趣的拓展阅读链接:
- A Few Useful Things to Know about Machine Learning,文中第6节与本节相关,但是整篇文章都强烈推荐。
- Recognizing and Learning Object Categories,ICCV 2005上的一节关于物体分类的课程。
9. 作业:k-Nearest Neighbor (kNN)
该assignment作业的官方说明地址(Q1: k-Nearest Neighbor classifier)
内含数据集下载办法,环境版本支持信息。
- 首先,初始化一些代码:
import random
import numpy as np
from cs231n.data_utils import load_CIFAR10
import matplotlib.pyplot as plt
from __future__ import print_function
# This is a bit of magic to make matplotlib figures appear inline in the notebook
# rather than in a new window.
#这里有一个小技巧可以让matplotlib画的图出现在notebook页面上,而不是新建一个画图窗口
%matplotlib inline
# set default size of plots 设置默认的绘图窗口大小
plt.rcParams['figure.figsize'] = (10.0, 8.0)
plt.rcParams['image.interpolation'] = 'nearest' # 差值方式
plt.rcParams['image.cmap'] = 'gray' # 灰度空间
# Some more magic so that the notebook will reload external python modules;
# see http://stackoverflow.com/questions/1907993/autoreload-of-modules-in-ipython
#另一个小技巧,下面的语句会让notebook自动加载最新版本的外部python模块
#详情见 http://stackoverflow.com/questions/1907993/autoreload-of-modules-in-ipython
%load_ext autoreload
%autoreload 2
There is a trick: when you forget all of the meaning of autoreload when using ipython, just try:
import autoreload
?autoreload
- 加载数据源:
# Load the raw CIFAR-10 data.
# 这里加载数据源的方法在data_utils.py中,会将data_batch_!到5的数据作为训练集,test_batch作为测试集
cifar10_dir = 'cs231n/datasets/cifar-10-batches-py'
X_train, y_train, X_test, y_test = load_CIFAR10(cifar10_dir)
# As a sanity check, we print out the size o f the training and test data.
# 检查一下数据,打印训练集及其标签和测试集及其标签的大小
print('Training data shape: ', X_train.shape)
print('Training labels shape: ', y_train.shape)
print('Test data shape: ', X_test.shape)
print('Test labels shape: ', y_test.shape)
# 返回值是:
# Training data shape: (50000, 32, 32, 3)
# Training labels shape: (50000,)
# Test data shape: (10000, 32, 32, 3)
# Test labels shape: (10000,)
- 来看看数据集都长什么样:
# Visualize some examples from the dataset.
# We show a few examples of training images from each class.
# 这里我们将训练集中每一个类别的样本随机挑出几个进行展示
classes = ['plane', 'car', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck']
num_classes = len(classes) # 类别数目
samples_per_class = 7 # 每个类别采样个数
# 对列表的元素位置和元素进行循环:
for y, cls in enumerate(classes): # 这里对应生成的是 (y, cls) = (0, plane), (1, car), (2, bird), ..., (9, truck)
# 在循环每一个类别时,挑出测试集y中该类别图片的索引位置(index):
idxs = np.flatnonzero(y_train == y)
# np.flatnonzero函数:返回扁平化后矩阵中非零元素(或真值)的位置索引(index)
# 随机从idxs中选取num_classes个数的内容,并将选取结果生成新的array中返回
idxs = np.random.choice(idxs, samples_per_class, replace=False)
for i, idx in enumerate(idxs): # 同上,i表示循环idx的序列号,idx是idxs的元素之一
plt_idx = i * num_classes + y + 1 # 在子图中所占位置的计算,竖着一列一列画的。
plt.subplot(samples_per_class, num_classes, plt_idx) # 说明要画的子图的编号
plt.imshow(X_train[idx].astype('uint8')) # show出image
plt.axis('off')
if i == 0:
plt.title(cls) # 每当画第一行图像时,写上标题,也就是类别名
plt.show()
# REF:http://www.cnblogs.com/lijiajun/p/5479523.html

- 数据准备
# Subsample the data for more efficient code execution in this exercise
# 为了更高效地运行我们的代码,这里取出一个子集进行后面的练习(取训练集前50000个,测试集前500个)
num_training = 5000
mask = list(range(num_training))
X_train = X_train[mask]
y_train = y_train[mask]
num_test = 500
mask = list(range(num_test))
X_test = X_test[mask]
y_test = y_test[mask]
(下面这一步可以省)
# Reshape the image data into rows
# 将图像数据转置成二维的
X_train = np.reshape(X_train, (X_train.shape[0], -1))
X_test = np.reshape(X_test, (X_test.shape[0], -1))
# 这里的-1表示,X_train.shape[0]作为新array的行数后,剩余可自动推断出的列数。
print(X_train.shape, X_test.shape)
# 打印结果:
# (5000, 3072) (500, 3072)
- 训练模型
We would now like to classify the test data with the kNN classifier. Recall that we can break down this process into two steps: 现在我们可以使用kNN分类器对测试样本进行分类了。我们可以将预测过程分为以下两步:
First we must compute the distances between all test examples and all train examples.
首先,我们需要计算测试样本和所有训练样本的距离。
Given these distances, for each test example we find the k nearest examples and have them vote for the label
得到距离矩阵后,找出离测试样本最近的k个训练样本,选择出现次数最多的类别作为测试样本的类别
Lets begin with computing the distance matrix between all training and test examples. For example, if there are Ntr training examples and Nte test examples, this stage should result in a Nte x Ntr matrix where each element (i,j) is the distance between the i-th test and j-th train example. 首先,计算距离矩阵。如果训练样本有Ntr个,测试样本有Nte个,则距离矩阵应该是个Nte x Ntr大小的矩阵,其中元素[i,j]表示第i个测试样本到第j个训练样本的距离。
First, open cs231n/classifiers/k_nearest_neighbor.py and implement the function compute_distances_two_loops that uses a (very inefficient) double loop over all pairs of (test, train) examples and computes the distance matrix one element at a time.
下面,打开cs231n/classifiers/k_nearest_neighbor.py,并补全compute_distances_two_loops方法,它使用了一个两层循环的方式(非常低效)计算测试样本与训练样本的距离.
from cs231n.classifiers import KNearestNeighbor
# Create a kNN classifier instance.
# Remember that training a kNN classifier is a noop:
# the Classifier simply remembers the data and does no further processing
classifier = KNearestNeighbor()
classifier.train(X_train, y_train)
- 模型测试
# Open cs231n/classifiers/k_nearest_neighbor.py and implement
# compute_distances_two_loops.
# 打开cs231n/classifiers/k_nearest_neighbor.py,补全compute_distances_two_loops方法
# Test your implementation:
# 测试一下
dists = classifier.compute_distances_two_loops(X_test)
print(dists.shape)
# 打印结果:
# (500, 5000) 其dists[i,j]表示的是第i个测试图片与第j个训练图片之间的L2距离
- 距离矩阵可视化
# We can visualize the distance matrix: each row is a single test example and
# its distances to training examples
# 我们可以将距离矩阵进行可视化:其中每一行表示一个测试样本与所有训练样本的距离
plt.imshow(dists, interpolation='none')
plt.show()

Inline Question #1: Notice the structured patterns in the distance matrix, where some rows or columns are visible brighter. (Note that with the default color scheme black indicates low distances while white indicates high distances.)
问个小问题 #1: 图中可以明显看出,行列之间有颜色深浅之分。(其中深色表示距离值小,而浅色表示距离值大)
What in the data is the cause behind the distinctly bright rows?
什么原因导致图中某些行的颜色明显偏浅?
What causes the columns?
为什么某些列的颜色明显偏浅?
Your Answer: fill this in.
你的答案: 写在这里。
- 测试样本与训练集中的样本差异较大,该测试样本可能是其他类别的图片,或者是一个异常图片
- 所有测试样本与该列表示的训练样本L2距离都较大
# Now implement the function predict_labels and run the code below:
# We use k = 1 (which is Nearest Neighbor).
# 实现predict_labels方法,然后运行下列代码
# 这里我们将k设置为1
y_test_pred = classifier.predict_labels(dists, k=1)
# Compute and print the fraction of correctly predicted examples
# 计算并打印准确率
num_correct = np.sum(y_test_pred == y_test)
accuracy = float(num_correct) / num_test
print('Got %d / %d correct => accuracy: %f' % (num_correct, num_test, accuracy))
# 打印结果:
# Got 137 / 500 correct => accuracy: 0.274000
You should expect to see approximately 27% accuracy. Now lets try out a larger k, say k = 5:
结果应该约为27%。现在,我们将k调大一点试试,令k = 5:
y_test_pred = classifier.predict_labels(dists, k=5)
num_correct = np.sum(y_test_pred == y_test)
accuracy = float(num_correct) / num_test
print('Got %d / %d correct => accuracy: %f' % (num_correct, num_test, accuracy))
# 打印结果:
# Got 139 / 500 correct => accuracy: 0.278000
You should expect to see a slightly better performance than with k = 1.
结果应该略好于k=1时的情况。
# Now lets speed up distance matrix computation by using partial vectorization
# with one loop. Implement the function compute_distances_one_loop and run the
# code below:
# 现在我们将距离计算的效率提升一下,使用单层循环结构的计算方法。实现
# compute_distances_one_loop方法,并运行下列代码
dists_one = classifier.compute_distances_one_loop(X_test)
# To ensure that our vectorized implementation is correct, we make sure that it
# agrees with the naive implementation. There are many ways to decide whether
# two matrices are similar; one of the simplest is the Frobenius norm. In case
# you haven't seen it before, the Frobenius norm of two matrices is the square
# root of the squared sum of differences of all elements; in other words, reshape
# the matrices into vectors and compute the Euclidean distance between them.
# 为了保证矢量化的代码运行正确,我们将运行结果与前面的方法的结果进行对比。对比两个
# 矩阵是否相等的方法有很多,比较简单的一种是使用Frobenius范数。Frobenius范数表示的
# 是两个矩阵所有元素的插值的平方和的根。或者说是将两个矩阵reshape成矢量后,它们之
# 间的欧氏距离
difference = np.linalg.norm(dists - dists_one, ord='fro')
print('Difference was: %f' % (difference, ))
if difference < 0.001:
print('Good! The distance matrices are the same')
else:
print('Uh-oh! The distance matrices are different')
# 打印结果:
# Difference was: 0.000000
# Good! The distance matrices are the same
# Now implement the fully vectorized version inside compute_distances_no_loops
# and run the code
# 完成完全矢量化方式运行的compute_distances_no_loops方法,并运行下列代码
dists_two = classifier.compute_distances_no_loops(X_test)
# check that the distance matrix agrees with the one we computed before:
# 将结果与之前的计算结果进行对比
difference = np.linalg.norm(dists - dists_two, ord='fro')
print('Difference was: %f' % (difference, ))
if difference < 0.001:
print('Good! The distance matrices are the same')
else:
print('Uh-oh! The distance matrices are different')
# 打印结果:
# Difference was: 0.000000
# Good! The distance matrices are the same
# Let's compare how fast the implementations are
# 下面我们对比一下各方法的执行速度
def time_function(f, *args):
"""
Call a function f with args and return the time (in seconds) that it took to execute.
"""
import time
tic = time.time()
f(*args)
toc = time.time()
return toc - tic
two_loop_time = time_function(classifier.compute_distances_two_loops, X_test)
print('Two loop version took %f seconds' % two_loop_time)
one_loop_time = time_function(classifier.compute_distances_one_loop, X_test)
print('One loop version took %f seconds' % one_loop_time)
no_loop_time = time_function(classifier.compute_distances_no_loops, X_test)
print('No loop version took %f seconds' % no_loop_time)
# 打印结果:
# Two loop version took 57.122203 seconds
# One loop version took 71.512672 seconds
# No loop version took 0.510630 seconds
# you should see significantly faster performance with the fully vectorized implementation
# 你应该可以看到,完全矢量化的代码运行效率有明显的提高
9.1 Cross-validation
We have implemented the k-Nearest Neighbor classifier but we set the value k = 5 arbitrarily. We will now determine the best value of this hyperparameter with cross-validation.
9.2 交叉验证
之前我们已经完成了k-Nearest分类器的编写,但是对于k值的选择很随意。下面我们将使用交叉验证的方法选择最优的超参数k。
num_folds = 5
k_choices = [1, 3, 5, 8, 10, 12, 15, 20, 50, 100]
X_train_folds = []
y_train_folds = []
################################################################################
# TODO: #
# Split up the training data into folds. After splitting, X_train_folds and #
# y_train_folds should each be lists of length num_folds, where #
# y_train_folds[i] is the label vector for the points in X_train_folds[i]. #
# Hint: Look up the numpy array_split function. #
# 任务: #
# 将训练数据切分成不同的折。切分之后,训练样本和对应的样本标签被包含在数组 #
# X_train_folds和y_train_folds之中,数组长度是折数num_folds。其中 #
# y_train_folds[i]是一个矢量,表示矢量X_train_folds[i]中所有样本的标签 #
# 提示: 可以尝试使用numpy的array_split方法。 #
################################################################################
X_train_folds = np.array_split(X_train, num_folds)
y_train_folds = np.array_split(y_train, num_folds)
# 以num_folds的折数从前向后分割,最后不够num_folds数目的为最后一折
################################################################################
# END OF YOUR CODE #
# 结束 #
################################################################################
# A dictionary holding the accuracies for different values of k that we find
# when running cross-validation. After running cross-validation,
# k_to_accuracies[k] should be a list of length num_folds giving the different
# accuracy values that we found when using that value of k.
# 我们将不同k值下的准确率保存在一个字典中。交叉验证之后,k_to_accuracies[k]保存了
# k值下,一个长度为折数的准确率矢量
k_to_accuracies = {}
for k in k_choices:
k_to_accuracies.setdefault(k, [])
################################################################################
# TODO: #
# Perform k-fold cross validation to find the best value of k. For each #
# possible value of k, run the k-nearest-neighbor algorithm num_folds times, #
# where in each case you use all but one of the folds as training data and the #
# last fold as a validation set. Store the accuracies for all fold and all #
# values of k in the k_to_accuracies dictionary. #
# 任务: #
# 通过k折的交叉验证找到最佳k值。对于每一个k值,执行kNN算法num_folds次,每一次 #
# 执行中,选择一折为训练集,最后一折为验证集。将不同k值在不同折上的运算结果保 #
# 存在k_to_accuracies字典中。 #
################################################################################
for i in range(num_folds):
classifier = KNearestNeighbor()
X_train_ = np.vstack(X_train_folds[:i] + X_train_folds[i+1:])
y_train_ = np.hstack(y_train_folds[:i] + y_train_folds[i+1:])
classifier.train(X_train_, y_train_)
for k in k_choices:
y_pred_ = classifier.predict(X_train_folds[i], k=k)
accuracy = np.mean(y_pred_ == y_train_folds[i])
k_to_accuracies[k].append(accuracy)
################################################################################
# END OF YOUR CODE #
################################################################################
# Print out the computed accuracies
for k in sorted(k_to_accuracies):
for accuracy in k_to_accuracies[k]:
print('k = %d, accuracy = %f' % (k, accuracy))
# plot the raw observations
# 画个图会更直观一点
for k in k_choices:
accuracies = k_to_accuracies[k]
plt.scatter([k] * len(accuracies), accuracies)
# plot the trend line with error bars that correspond to standard deviation
# 画出在不同k值下,误差均值和标准差
accuracies_mean = np.array([np.mean(v) for k,v in sorted(k_to_accuracies.items())])
accuracies_std = np.array([np.std(v) for k,v in sorted(k_to_accuracies.items())])
plt.errorbar(k_choices, accuracies_mean, yerr=accuracies_std)
plt.title('Cross-validation on k')
plt.xlabel('k')
plt.ylabel('Cross-validation accuracy')
plt.show()
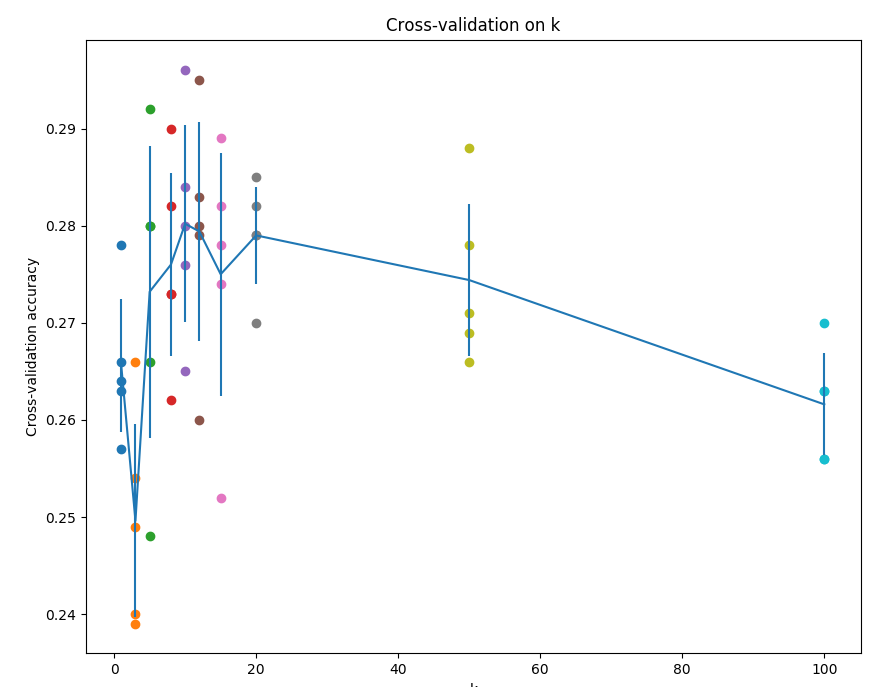
# Based on the cross-validation results above, choose the best value for k,
# retrain the classifier using all the training data, and test it on the test
# data. You should be able to get above 28% accuracy on the test data.
# 根据上面交叉验证的结果,选择最优的k,然后在全量数据上进行试验,你将得到约28%的准确率
best_k = 6
classifier = KNearestNeighbor()
classifier.train(X_train, y_train)
y_test_pred = classifier.predict(X_test, k=best_k)
# Compute and display the accuracy
# 计算并展示准确率
num_correct = np.sum(y_test_pred == y_test)
accuracy = float(num_correct) / num_test
print('Got %d / %d correct => accuracy: %f' % (num_correct, num_test, accuracy))
# 打印结果:
# Got 141 / 500 correct => accuracy: 0.282000
9.3 k_nearest_neighbor.py
#-*- coding:utf-8 -*-
import numpy as np
#from past.builtins import xrange
class KNearestNeighbor(object):
""" a kNN classifier with L2 distance """
""" 使用L2距离的kNN分类器 """
def __init__(self):
pass
def train(self, X, y):
"""
Train the classifier. For k-nearest neighbors this is just
memorizing the training data.
Inputs:
- X: A numpy array of shape (num_train, D) containing the training data
consisting of num_train samples each of dimension D.
- y: A numpy array of shape (N,) containing the training labels, where
y[i] is the label for X[i].
训练分类器。对于KNN分类器来说,训练就是将训练数据保存
输入:
-X: 训练数据集,一个(训练样本数量,维度)大小的numpy数组
-y: 训练样本标签,一个(训练样本数量,1)大小的numpy数组,其中y[i]表示样本X[i]的类别标签
"""
self.X_train = X
self.y_train = y
def predict(self, X, k=1, num_loops=0):
"""
Predict labels for test data using this classifier.
Inputs:
- X: A numpy array of shape (num_test, D) containing test data consisting
of num_test samples each of dimension D.
- k: The number of nearest neighbors that vote for the predicted labels.
- num_loops: Determines which implementation to use to compute distances
between training points and testing points.
Returns:
- y: A numpy array of shape (num_test,) containing predicted labels for the
test data, where y[i] is the predicted label for the test point X[i].
该方法对输入数据进行类别预测
输入:
- X: 测试数据集,一个(测试样本数量,维度)大小的numpy数组
- k: 最近邻数量
- num_loops: 计算测试样本和训练样本距离的方法
返回:
- y: 类别预测结果,一个(测试样本数量,1)大小的numpy数组,其中y[i]是样本X[i]的预测结果
"""
if num_loops == 0:
dists = self.compute_distances_no_loops(X)
elif num_loops == 1:
dists = self.compute_distances_one_loop(X)
elif num_loops == 2:
dists = self.compute_distances_two_loops(X)
else:
raise ValueError('Invalid value %d for num_loops' % num_loops)
return self.predict_labels(dists, k=k)
def compute_distances_two_loops(self, X):
"""
Compute the distance between each test point in X and each training point
in self.X_train using a nested loop over both the training data and the
test data.
Inputs:
- X: A numpy array of shape (num_test, D) containing test data.
Returns:
- dists: A numpy array of shape (num_test, num_train) where dists[i, j]
is the Euclidean distance between the ith test point and the jth training
point.
通过一个两层的嵌套循环,遍历测试样本点,并求其到全部训练样本点的距离
输入:
- X: 测试数据集,一个(测试样本数量, 维度)大小的numpy数组
返回:
- dists: 一个(测试样本数量, 训练样本数量) 大小的numpy数组,其中dists[i, j]
表示测试样本i到训练样本j的欧式距离
"""
num_test = X.shape[0]
num_train = self.X_train.shape[0]
dists = np.zeros((num_test, num_train))
for i in range(num_test):
for j in range(num_train):
#####################################################################
# TODO: #
# Compute the l2 distance between the ith test point and the jth #
# training point, and store the result in dists[i, j]. You should #
# not use a loop over dimension. #
# 任务: #
# 计算第i个测试点到第j个训练样本点的L2距离,并保存到dists[i, j]中, #
# 注意不要在维度上使用for循环 #
#####################################################################
dists[i, j] = np.sqrt(np.sum(np.square(self.X_train[j,:] - X[i,:])))
# 这里的np.square()是对其中每个元素平方操作
#####################################################################
# END OF YOUR CODE #
# 任务结束 #
#####################################################################
return dists
def compute_distances_one_loop(self, X):
"""
Compute the distance between each test point in X and each training point
in self.X_train using a single loop over the test data.
Input / Output: Same as compute_distances_two_loops
通过一个单层的嵌套循环,遍历测试样本点,并求其到全部训练样本点的距离
输入/输出:和compute_distances_two_loops方法相同
"""
num_test = X.shape[0]
num_train = self.X_train.shape[0]
dists = np.zeros((num_test, num_train))
for i in range(num_test):
#######################################################################
# TODO: #
# Compute the l2 distance between the ith test point and all training #
# points, and store the result in dists[i, :]. #
# 任务: #
# 计算第i个测试样本点到所有训练样本点的L2距离,并保存到dists[i, :]中 #
#######################################################################
dists[i,:] = np.sqrt(np.sum(np.square(self.X_train - X[i,:]),axis = 1))
#######################################################################
# END OF YOUR CODE #
# 任务结束 #
#######################################################################
return dists
def compute_distances_no_loops(self, X):
"""
Compute the distance between each test point in X and each training point
in self.X_train using no explicit loops.
Input / Output: Same as compute_distances_two_loops
不通过循环方式,遍历测试样本点,并求其到全部训练样本点的距离
输入/输出:和compute_distances_two_loops方法相同
"""
num_test = X.shape[0]
num_train = self.X_train.shape[0]
dists = np.zeros((num_test, num_train))
#########################################################################
# TODO: #
# Compute the l2 distance between all test points and all training #
# points without using any explicit loops, and store the result in #
# dists. #
# #
# You should implement this function using only basic array operations; #
# in particular you should not use functions from scipy. #
# #
# HINT: Try to formulate the l2 distance using matrix multiplication #
# and two broadcast sums. #
# 任务: #
# 计算测试样本点和训练样本点之间的L2距离,并且不使用for循环,最后将结果 #
# 保存到dists中 #
# #
# 请使用基本的数组操作完成该方法;另外,不要使用scipy中的方法 #
# #
# 提示: 可以使用矩阵乘法和两次广播加法 #
#########################################################################
# 这里对完全平方公式做了展开,以方便我们实现矢量化,(a-b)^2=a^2+b^2-2ab
dists = np.sqrt(-2*np.dot(X, self.X_train.T) # 一个500*5000的矩阵
+ np.sum(np.square(self.X_train), axis=1) # 一个1*5000的矩阵
+ np.transpose([np.sum(np.square(X), axis=1)])) # 一个500*1的矩阵
# 留意self.X_train的shape是(5000,3072),X的shape是(500,3072)
# np.dot()是矩阵乘法, np.sqrt()和np.square()都是对矩阵每个元素的操作
# np.sum(array_like, axis=1)是对矩阵每行分别求和,即每个图片像素求和
# 注意:后两个矩阵的加法可以张成一个500*5000的矩阵!
#########################################################################
# END OF YOUR CODE #
# 任务结束 #
#########################################################################
return dists
def predict_labels(self, dists, k=1):
"""
Given a matrix of distances between test points and training points,
predict a label for each test point.
Inputs:
- dists: A numpy array of shape (num_test, num_train) where dists[i, j]
gives the distance betwen the ith test point and the jth training point.
Returns:
- y: A numpy array of shape (num_test,) containing predicted labels for the
test data, where y[i] is the predicted label for the test point X[i].
通过距离矩阵,预测每一个测试样本的类别
输入:
- dists: 一个(测试样本数量,训练样本数量)大小的numpy数组,其中dists[i, j]表示
第i个测试样本到第j个训练样本的距离
返回:
- y: 一个(测试样本数量,)大小的numpy数组,其中y[i]表示测试样本X[i]的预测结果
"""
num_test = dists.shape[0]
y_pred = np.zeros(num_test)
for i in range(num_test):
# A list of length k storing the labels of the k nearest neighbors to
# the ith test point.
# 一个长度为k的list数组,其中保存着第i个测试样本的k个最近邻的类别标签
closest_y = []
#########################################################################
# TODO: #
# Use the distance matrix to find the k nearest neighbors of the ith #
# testing point, and use self.y_train to find the labels of these #
# neighbors. Store these labels in closest_y. #
# Hint: Look up the function numpy.argsort. #
# 任务: #
# 通过距离矩阵找到第i个测试样本的k个最近邻,然后在self.y_train中找到这些 #
# 最近邻对应的类别标签,并将这些类别标签保存到closest_y中。 #
# 提示: 可以尝试使用numpy.argsort方法 #
#########################################################################
# 在dists距离矩阵中,第i个测试图片(第i行)下的列(训练图片),按值从小到大排列,
# 取出前k个的索引(原列数,亦训练集的索引),最后根据该索引在测试集中切片出相应的标签值
closest_y = self.y_train[np.argsort(dists[i])[:k]]
# np.argsort()函数返回的是数组值从小到大的索引值
#########################################################################
# TODO: #
# Now that you have found the labels of the k nearest neighbors, you #
# need to find the most common label in the list closest_y of labels. #
# Store this label in y_pred[i]. Break ties by choosing the smaller #
# label. #
# 任务: #
# 现在你已经找到了k个最近邻对应的标签, 下面就需要找到其中最普遍的那个 #
# 类别标签,然后保存到y_pred[i]中。如果有票数相同的类别,则选择编号小 #
# 的类别 #
#########################################################################
y_pred[i] = np.argmax(np.bincount(closest_y))
# np.bincount()是凡是与索引值相同的值,计数+1,计数结果返回为新的索引值里的计数值
# np.argmax() 返回的是数值最大的索引值,在这个例子中即是标签
#########################################################################
# END OF YOUR CODE #
#########################################################################
return y_pred