S_Dbw 聚类评估指标(代码全解析)
S_Dbw算法的原论文地址:Clustering Validity Assessment: Finding the optimal partitioning of a data set本文算法的 Rep 地址:https://github.com/iphysresearch/S_Dbw_validity_index
此文的 motivation 来自于近期接的某无监督 k-means 聚类项目,并计划是用基于 K-means 算法的 k-prototypes 聚类算法来打发了事。为了对聚类结果给出合理靠谱的评估评价,最终决定主要参考 S_Dbw 评估指标,并且打算写作此文,非原理性的解析 S_Dbw,原因有二:
- 在2001年有一篇引用率挺高(300+)的 paper 1谈到说,
S_Dbw聚类评价指标对于各种噪声,不同密度的数据集等等干扰项来调参的鲁棒性最强,直接完爆其他所有评价指标~ S_Dbw算法在 sciki-learn 中至今(2018)还没有被添加到 api 中 2,相比,R 语言里却有现成且很好的 api 可以调用,如clv和NbClust3。关于S_Dbw算法现成的 Python 代码版本,在网络上也难以寻觅,唯一的参考是 fanfanda 的 版本。不过,此代码应该是有问题的,它聚类中心的定义是有误的。
综上,自己决定在 fanfanda 的代码基础上修正代码,并且贴出此代码算法的详细解析。
注:符号完全参考论文原文,且已尽可能的说明算法的内涵和代码实现原理,更详细信息请参阅原论文。
import numpy as np
我们先给出数学上的预定义:说 $D = {\nu_i|i_1,\dots,c}$ 是一个针对数据集 S 的划分,分成了 c 个类,其中的 $\nu_i$ 就是第 $i$ 类的中心。
下面定义类 S_Dbw,并且可以看到,算法的输入信息有三个方面:数据集+聚类结果+各聚类类别的"中心"
class S_Dbw():
def __init__(self,data,data_cluster,cluster_centroids_):
"""
data --> raw data
data_cluster --> The category that represents each piece of data(the number of category should begin 0)
cluster_centroids_ --> the center_id of each cluster's center
"""
self.data = data
self.data_cluster = data_cluster
self.cluster_centroids_ = cluster_centroids_
# cluster_centroids_ 是一个 array, 给出类数k
self.k = cluster_centroids_.shape[0]
self.stdev = 0 # stdev 的初始化
# 对每个类别标记进行循环,如:0,1,2,...
# 该循环计算的是下面公式里根号里的内容:
for i in range(self.k):
# 计算某类别下所有样本各自的全部特征值的方差:
#(vector,shape为样本的个数,相当于下面公式里的 signma)
std_matrix_i = np.std(data[self.data_cluster == i],axis=0)
# 求和
self.stdev += np.sqrt(np.dot(std_matrix_i.T,std_matrix_i))
self.stdev = np.sqrt(self.stdev)/self.k # 取平均
在上面的初始化中,我们定义了一个叫做 stdev 的变量,定义为每个类的平均标准方差:
$$stdev = \frac{1}{c}\sqrt{\sum^c_{i=1}||\sigma(\nu_i)||}$$
其中,符号 $||\cdot||$ 表示为 $||\mathbf{x}||=(\mathbf{x}^T\mathbf{x})^{1/2}$ (矢量的欧式距离,或者说白了,就是高维空间中坐标两点之间的欧氏距离)。
下面开始计算所谓的 Inter-cluster Density(ID),即要定义的 Dens_bw 函数。但在此之前,需要先行考量计算的是一个关于两个类之间的 density,定义如下:
$$ density(u)=\sum^{n_{ij}}{l=1}f(x_l,u), ,\text{where } n{ij}= \text{ number of tuples} $$
其中,$x_l$ 是以 $u$ 为邻域内的样本个数,显然这个样本数目肯定不会超过两个类的合并,更不会超过整个数据量,也就是说满足:$x_l\in c_i\cup c_j \subseteq S$。所以说,上面的公式针对两个类别样本,只要给定一个邻域范围 $u$,就可以给出一个 scalar 来表征密度的含义。那么 $u$ 怎么定义?表征密度的 $f$ 函数又怎么定义呢?说来就来,立马给你定义!
$$f(x,u) = \begin{cases} 0,& \text{if } d(x,u)>stdev\\ 1,& \text{otherwise}.\end{cases}$$
这是啥意思呢?
上面定义过的 stdev 相当于是给每个聚类类别定义了一个“单位圆“作为标准。$f$ 函数所做的事情就是数数啊,假如考虑的是某单类 $i$ 里的 $density(\nu_i)$,那就去数究竟有多少个样本可以落到该聚类类别中心点外 $\nu_i$ 的这个标准范围 stdev 内。如果说是像上面某两个类 $(i,j)$ 的 $density(u_{ij})$ 的情况话,也简单,把这两个类中的中心点当做新的中心,再看它附近”单位圆“里有多少个样本。
值得注意的是,我刚刚用了”圆“这个词,其实也就是暗示了每个样本的维度是 comparable 的。也就是说数据至少要做过标准化才行哦~ 最好也是正态化好的。
下面就是这个 density(density_list=[]) 函数的定义了:
def density(self,density_list=[]):
"""
compute the density of one or two cluster(depend on density_list)
变量 density_list 将作为此函数的内部列表,其取值范围是0,1,2,... ,元素个数是聚类类别数目
"""
density = 0
if len(density_list) == 2: # 当考虑两个聚类类别时候,给出中心点位置
center_v = (self.cluster_centroids_[density_list[0]] +self.cluster_centroids_[density_list[1]])/2
else: # 当只考虑某一个聚类类别的时候,给出中心点位置
center_v = self.cluster_centroids_[density_list[0]]
for i in density_list:
temp = self.data[self.data_cluster == i]
for j in temp: # np.linalg.norm 是求范数(order=2)
if np.linalg.norm(j - center_v) <= self.stdev:
density += 1
return density
定义完 density() ,我们就终于可以给出 Inter-cluster Density(ID),即要定义的 Dens_bw 函数:
$$ \text{Dens_bw}(c) = \frac{1}{c\cdot(c-1)}\sum^c_{i=1}\left(\sum^c_{j=1,j\neq i} \frac{density(u_{ij})}{\max{density(\nu_i),density(\nu_j)}}\right) $$
这个时候,上面的公式就好读多了。
大括号里有很多项是加起来的,每一项对应于在所有聚类类别中,两两匹配且有序不重复的去穷举(所谓“排列”规则,如6个里面取2个就有 $6^2$ 种取法)。其中分子是两个聚类类别合在一起的密度,再除以该两个聚类类别里密度相对最大的那个。可见,如果两个聚类中心分得很开,同时每个类还各自密度很高很紧凑,那么分子就越小(两个类中心的中点处密度甚至可能为0),分母就越大(显然每类越紧凑,密度越大嘛)。所以,由此可见一斑,这个评估指标是越小越好啊!
下面的代码对应的就是上面公式 Dens_bw:
def Dens_bw(self):
density_list = []
result = 0
# 下面的变量 density_list 列表将会算出每个对应单类的密度值。
for i in range(self.k):
density_list.append(self.density(density_list=[i])) # i 是循环类别标签
# 开始循环排列
for i in range(self.k):
for j in range(self.k):
if i==j:
continue
result += self.density([i,j])/max(density_list[i],density_list[j])
return result/(self.k*(self.k-1))
我们把 Dens_bw 定义好后,任务只能说是刚过半。接下来要把另一半定义清楚,即Intra-cluster variance ,所谓对 average scattering 的衡量,定义为 Scat() 函数:
$$ \text{Scat}(c) = \frac{1}{c}\sum^c_{i=1}\frac{||\sigma(\nu_i)||}{||\sigma(S)||} $$
上式中,$||\sigma(S)||$ 表示的是整个样本数据 $S$ 的方差,那么 $||\sigma(\nu_i)||$ 表示的就是第 $i$ 类样本数据的方差。一个数列的方差我们很清楚,俺么话说一个二维数列的方差是什么鬼呢?原论文给出了详细的解释:不管是整个样本数据集 $S$ 还是其中的某一类样本数据集合 $\nu_i$。所谓方差,是对数据集合的每一列(每一个特征)求方差,得到一个维数为特征数目的向量 $\mathbf{x}$,然后就是如上法炮制去算该矢量的欧式距离 $||\mathbf{x}||$ 即可。
def Scat(self):
# 分母部分:
sigma_s = np.std(self.data,axis=0)
sigma_s_2norm = np.sqrt(np.dot(sigma_s.T,sigma_s))
# 分子部分:
sum_sigma_2norm = 0
for i in range(self.k):
matrix_data_i = self.data[self.data_cluster == i]
sigma_i = np.std(matrix_data_i,axis=0)
sum_sigma_2norm += np.sqrt(np.dot(sigma_i.T,sigma_i))
return sum_sigma_2norm/(sigma_s_2norm*self.k)
从上面的公式也可以晓得,如果所有的聚类类目在高维特征空间上散布的很开(即 $||\sigma(S)||$ 挺大的),同时每个聚类类别各自在空间中散布的很紧凑($||\sigma(\nu_i)||$都挺小),那不就说明聚类效果还不错,输出 Scat() 也就对应于一个较小的评估值。
综上呢,我们的 S_Dbw 聚类评估指标就是把 Dens_bw() 和 Scat() 的结果加起来,即可万事大吉:
def S_Dbw_result(self):
"""
compute the final result
"""
return self.Dens_bw()+self.Scat()
来个栗子,瞧一瞧!
- 固定住模拟数据的中心点,变化散布程度:
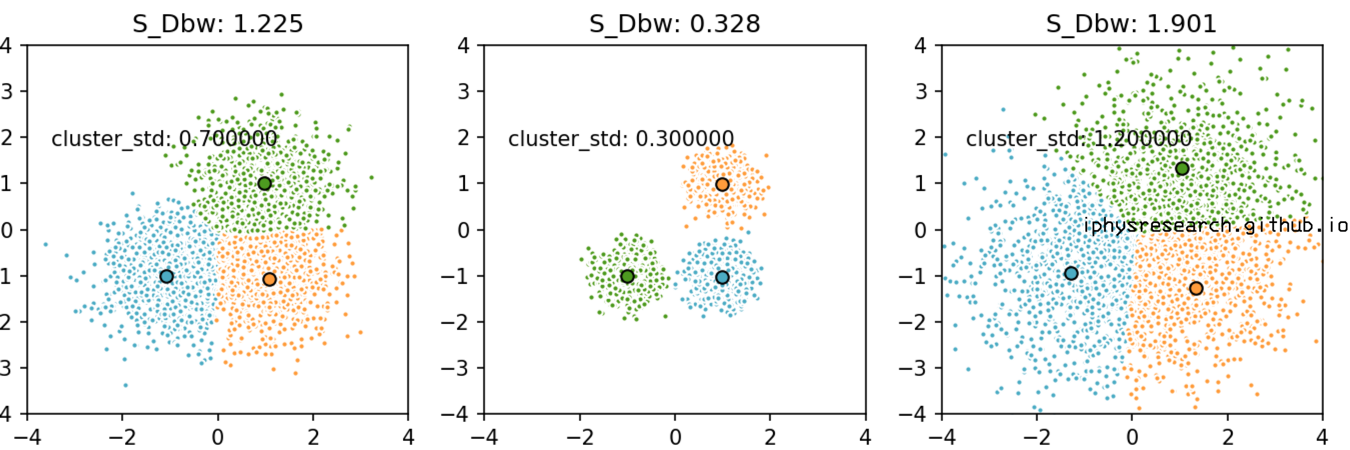
- 变化模拟数据的中心点,固定每类的散布程度:
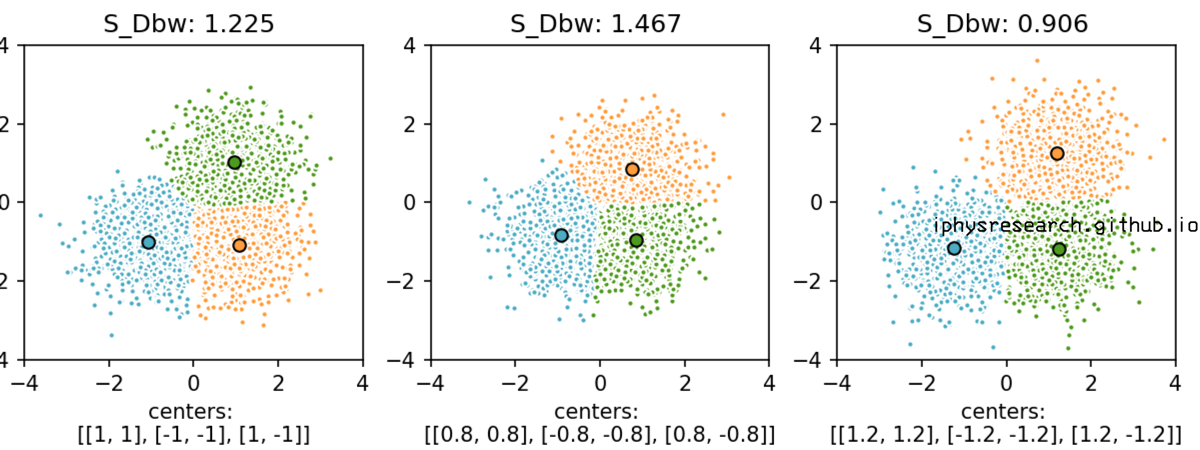
上面两个图的代码如下:
import numpy as np
import S_Dbw as sdbw
from sklearn.cluster import KMeans
from sklearn.datasets.samples_generator import make_blobs
from sklearn.metrics.pairwise import pairwise_distances_argmin
np.random.seed(0)
S_Dbw_result = []
batch_size = 45
centers = [[1, 1], [-1, -1], [1, -1]]
cluster_std=[0.7,0.3,1.2]
n_clusters = len(centers)
X1, _ = make_blobs(n_samples=3000, centers=centers, cluster_std=cluster_std[0])
X2, _ = make_blobs(n_samples=3000, centers=centers, cluster_std=cluster_std[1])
X3, _ = make_blobs(n_samples=3000, centers=centers, cluster_std=cluster_std[2])
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(9, 3))
fig.subplots_adjust(left=0.02, right=0.98, bottom=0.08, top=0.9)
colors = ['#4EACC5', '#FF9C34', '#4E9A06']
for item, X in enumerate(list([X1, X2, X3])):
k_means = KMeans(init='k-means++', n_clusters=3, n_init=10)
k_means.fit(X)
k_means_cluster_centers = k_means.cluster_centers_
k_means_labels = pairwise_distances_argmin(X, k_means_cluster_centers)
KS = sdbw.S_Dbw(X, k_means_labels, k_means_cluster_centers)
S_Dbw_result.append(KS.S_Dbw_result())
ax = fig.add_subplot(1,3,item+1)
for k, col in zip(range(n_clusters), colors):
my_members = k_means_labels == k
cluster_center = k_means_cluster_centers[k]
ax.plot(X[my_members, 0], X[my_members, 1], 'w',
markerfacecolor=col, marker='.')
ax.plot(cluster_center[0], cluster_center[1], 'o', markerfacecolor=col,
markeredgecolor='k', markersize=6)
ax.set_title('S_Dbw: %.3f' %(S_Dbw_result[item]))
ax.set_ylim((-4,4))
ax.set_xlim((-4,4))
plt.text(-3.5, 1.8, 'cluster_std: %f' %(cluster_std[item]))
plt.savefig('./pic1.png', dpi=150)
np.random.seed(0)
S_Dbw_result = []
batch_size = 45
centers = [[[1, 1], [-1, -1], [1, -1]],
[[0.8, 0.8], [-0.8, -0.8], [0.8, -0.8]],
[[1.2, 1.2], [-1.2, -1.2], [1.2, -1.2]]]
n_clusters = len(centers)
X1, _ = make_blobs(n_samples=3000, centers=centers[0], cluster_std=0.7)
X2, _ = make_blobs(n_samples=3000, centers=centers[1], cluster_std=0.7)
X3, _ = make_blobs(n_samples=3000, centers=centers[2], cluster_std=0.7)
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(8, 3))
fig.subplots_adjust(left=0.02, right=0.98, bottom=0.2, top=0.9)
colors = ['#4EACC5', '#FF9C34', '#4E9A06']
for item, X in enumerate(list([X1, X2, X3])):
k_means = KMeans(init='k-means++', n_clusters=3, n_init=10)
k_means.fit(X)
k_means_cluster_centers = k_means.cluster_centers_
k_means_labels = pairwise_distances_argmin(X, k_means_cluster_centers)
KS = sdbw.S_Dbw(X, k_means_labels, k_means_cluster_centers)
S_Dbw_result.append(KS.S_Dbw_result())
ax = fig.add_subplot(1,3,item+1)
for k, col in zip(range(n_clusters), colors):
my_members = k_means_labels == k
cluster_center = k_means_cluster_centers[k]
ax.plot(X[my_members, 0], X[my_members, 1], 'w',
markerfacecolor=col, marker='.')
ax.plot(cluster_center[0], cluster_center[1], 'o', markerfacecolor=col,
markeredgecolor='k', markersize=6)
ax.set_title('S_Dbw: %.3f ' %(S_Dbw_result[item]))
# ax.set_xticks(())
# ax.set_yticks(())
ax.set_ylim((-4,4))
ax.set_xlim((-4,4))
ax.set_xlabel('centers: \n%s' %(centers[item]))
plt.savefig('./pic2.png', dpi=150)