Python 中负数取余问题

最近发现在 Scipy 信号处理的原代码中，可以利用对负数取余的便利操作，进一步优化和清晰我们数据处理的过程。

官方 Python 文档中对 % 或者完全等价的 operator.mod() (需要import operator) 介绍不清楚，可以参考下面三个材料，写的非常好！

• Useful references
  • Python Modulo in Practice: How to Use the % Operator - Real Python
  • The Modulo Operation (%) With Negative Numbers in Python - Gonzalo Ferreiro Volpi
  • The modulo operation on negative numbers in Python - Stack Overflow

上面，是我搜集了 3 个与 % 相关的讲的非常详细细致的教程帖子。下面，我直接简明扼要的介绍这个 “负数取余” 的 trick。

例子：

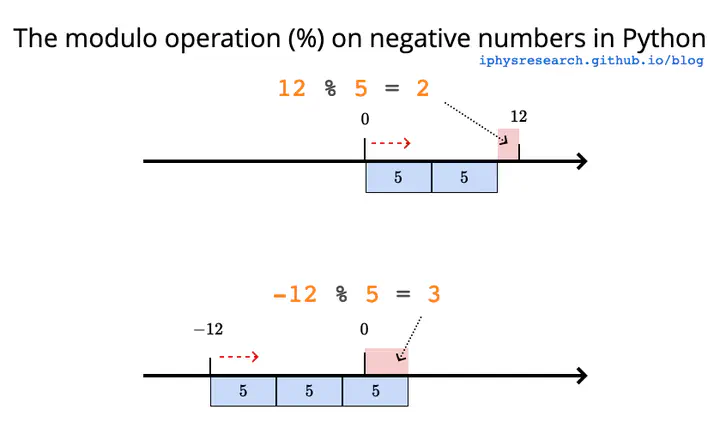
12 % 5, -12 % 5
# output
# (2, 3)

这是为什么呢？

在数学里，“负数取余"遵循的是：

如果 a 与 d 是整数，d 非零，那么余数 r 满足 a = q * d + r, q 为整数，且 0 <= |r| < |d|。

由此可见，我们的被除数 a = 12, 我们的商 d = 5，那么有两个余 r 满足条件，分别是一个负的余数 r1 = -2 和正的余数 r2 = 3，并且总有规律 r1 + r2 = d。

在计算机语言中，同号的整数运算，所有语言都遵循尽量让商小的原则，所以 12 mod 5 和 -12 mod -5 是一样的方式，结果差一个符号，分别是 2 和 -2。但是在异号的整数运算中，C 和 Java 都是尽可能让商 d 更大 ¹（例如 -12 mod 5 的结果对应的是商 d = -2，余 r = -2），而 Python 则是会让商尽可能的小（例如 -12 mod 5 的结果对应的是商 d = -3，余 r = 3）。

最近，在我阅读 scipy/signal/spectral.py 的源代码时，看到在数据处理中使用“负数取余”可以写出更加简洁和清晰的代码。由此，进而可以给出如下的一种更好的理解方式：

还是 -12 mod 5 这个例子：

所以，有时候我们为了对时序数据计算 padding 等问题的时候，可以考虑令其数据长度为负，再整除以 step 后，来计算“余出”部分的数据长度，而不是“欠余”部分的数据长度。