恒 Q 变换 (Constant-Q transform)
Understanding Constant-Q transform by Python
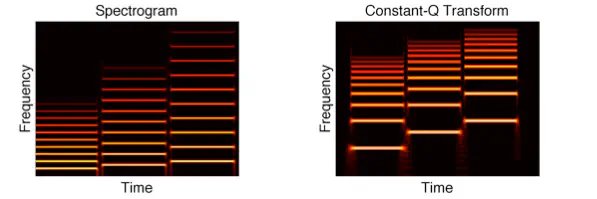 Credit by Gautham J. Mysore
Credit by Gautham J. Mysore由于在音乐中,所有的音都是由若干八度的 12 平均律共同组成的,这十二平均律对应着钢琴中一个八度上的十二个半音。这些半音临近之间频率比为 $2^{1/12}$。显然,同一音级的两个八度音,高八度音是低八度音频率的两倍。比方说,西方音乐的基频 (F0s) 可以如下定义:
$$ F_k = 440\text{Hz} \times 2^{k/12} $$ 其中,$k\in[-50,40]$ 是一个整数。
因此在音乐当中,声音都是以指数分布的,但我们的傅立叶变换得到的音频谱都是线性分布的,两者的频率点是不能一一对应的,这会指使某些音阶频率的估计值产生误差。所以现代对音乐声音的分析,一般都采用一种具有相同指数分布规律的时频变换算法—— CQT (Constant-Q transform)。
音频处理中的恒定Q变换,主要的应用在声源分离、音频谱分析及音频效果上。(Constant-Q transform in music processing. It is useful for several applications, including sound source separation, music signal analysis, and audio effects.)
什么是恒 Q 变换(CQT)
CQT 指中心频率按指数规律分布,滤波带宽不同、但中心频率与带宽比为常量 Q 的滤波器组。它与傅立叶变换不同的是,它频谱的横轴频率不是线性的,而是基于 $\log2$ 为底的,并且可以根据谱线频率的不同该改变滤波窗长度,以获得更好的性能。由于 CQT 与音阶频率的分布相同,所以通过计算音乐信号的 CQT 谱,可以直接得到音乐信号在各音符频率处的振幅值,对于音乐的信号处理来说简直完美。
CQT 变换没有得以广泛的得到应用有 4 个主要原因:
- 与 DFT 相比,它的计算效率是不行的;
- 缺少能够实现完美信号重构的逆 CQT 变换;
- CQT 的时频图像所表示的矩阵数据结构比短时傅里叶变换相比处理起来有难度;
- CQT 中,某确定的时间分辨率变化下会要计算不同的频域变换范围,换句话说要实现不同频率范围下的不同步采样。
关于信号处理中的窗口
在实际的信号处理过程中,我们会将时间片段分帧,按照帧为单位,转换成一个基于时间帧的频谱图,然后我们再将这些频谱图放到时间轴上,就可以形成一个类似热力图样的,基于时间变换的频谱变换图。
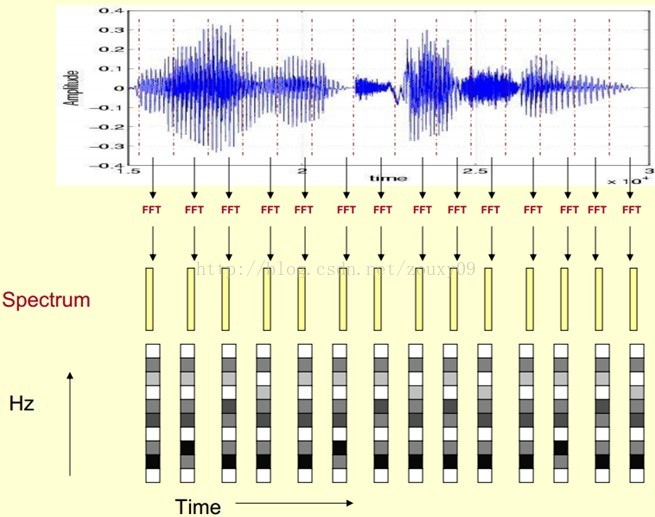
现在我们注意一个问题,在我们的单个时间帧内(实际上我们在对信号进行截断),信号很可能不呈现它原周期的整数倍(周期截断),那么截断后的信号会泄漏问题,为了更好地满足傅立叶变换(实际上是FFT)处理的周期性要求,我们需要使用加权函数,也叫窗函数 (windown function)。加窗主要是为了使时域信号似乎更好地满足FFT处理的周期性要求,减少泄漏。
我们关注上述“中心频率与带宽比为常量 Q”,从公式上看,我们可以表达为下述公式:
$$ Q = \frac{f_k}{\Delta f_k} . $$ 其中,filter width, $\Delta f_k$; $Q$, the “quality factor”.
直观的理解是,恒Q变换避免了时频分辨率均匀的缺点,对于低频的波,它的带宽十分小,但有更高的频率分辨率来分解相近的音符;但是对于高频的波,它的带宽比较大,在高频有更高的时间分辨率来跟踪快速变化的泛音。
CQT 变换 $X^\text{QT}(k, n)$ 关于离散时域信号 $x(n)$ 可以定义为:
$$ X^{\mathrm{CQ}}(k, n)=\sum_{j=n-\left\lfloor N_{k} / 2\right\rfloor}^{n+\left\lfloor N_{k} / 2\right\rfloor} x(j) a_{k}^{*}\left(j-n+N_{k} / 2\right) $$
其中,$k=1,2,\dots,K$ 表示的 CQT 变换的频域 bins,$\lfloor\cdot\rfloor$ 表示的是向下取整,$a^*_k(n)$ 表示的是对 $a_k(n)$ 的复共轭。可以看到,上面公式中的基函数 $a_k(n)$ 是一个复数域的波形,通常叫做时频原子 (atom),定义为:
$$ a_{k}(n)=\frac{1}{N_{k}} w\left(\frac{n}{N_{k}}\right) \exp \left[-i 2 \pi n \frac{f_{k}}{f_{\mathrm{s}}}\right] $$
其中,$f_k$ 就是第 $k$ 个 bin 的中心频率,$f_s$ 是采样率,而 $w(t)$ 是连续的窗函数 (比方说汉宁窗或者布莱克曼窗),窗函数在 $t\in[0,1]$ 以外恒为零。上面两个公式中的窗口跨度 $N_k\in\mathbb{R}$ 是与 $f_k$ 成反比的实数,即在所有的 bins $k$ 上为恒定的常量 Q。
中心频率 $f_k$ 满足关系:
$$ f_{k}=f_{1} 2^{\frac{k-1}{B}} $$
其中,$f_1$ 就是最低频率 bin 里的中心频率,而 $B$ 是每一个八度 (octave) 中所取的 bins 数目。显然,$B$ 这个参数是一个 CQT 中很重要的超参数,因为它决定了 CQT 在时频域上的分辨率。
每一个 bin $k$ 所对应的常量 Q 为:
$$ Q = Q_{k} \stackrel{\text { def. }}{=} \frac{f_{k}}{\Delta f_{k}}=\frac{N_{k} f_{k}}{\Delta \omega f_{s}} $$
其中,$\Delta f_{k}$ 是 atom $a_k(n)$ 的频域带宽相应,$\Delta \omega$ 是窗函数 $w(t)$ 的能谱带宽。
我们当然希望让 Q 可以越大越好,这样的话每个 bin 的带宽 $\Delta f_k$ 就可以越来越小。但是 Q 并不能任意的大,否则 bins 之间的部分能谱就会没法有效的分析。所以,给定 Q 值后,也就意味着给定的能够重构波形的最小频率带宽:
$$ Q=\frac{q}{\Delta \omega\left(2^{\frac{1}{B}}-1\right)} $$
其中,$0<q \lesssim 1$ 是一个缩放因子,通常来说我们取 $q=1$。$q$ 越小也就意味着提高了时间分辨率,而降低频率分辨率。需要注意的是,比方说 $q=0.5$ 和 $B=48$ 与 $q=1$ 和 $B=24$ 是等价的,而前者在每个八度中会有两倍的频域 bins 数目。也就是说,$q<1$ 意味着在频域进行了过采样 (oversampling),类似于通过零填充来计算 DFT 一样。比方说,$q=0.5$ 对应于 2 倍的过采样,这在每个八度范围中取了一个等效的 $B/2$ 个 bins 的频域分辨率,尽管每个八度里确实分了 $B$ 个 bins。
上面两个公式合在一起后,就可以给出 $N_k$:
$$ N_{k}=\frac{q f_{\mathrm{s}}}{f_{k}\left(2^{\frac{1}{B}}-1\right)} $$
这个公式很重要,可以看到公式中没有了 $\Delta \omega$。
Codes
对输入信号的每一个采样点 $n$ 都去计算其 CQT 变换系数 $X^\text{CQ}(k,n)$ 是难以实现的。Constant-Q transform toolbox for music processing 这个文章就是解决了这个问题。文章作者谈到说,他们不仅可以让 CQT 的运算效率很好的提升(通过稀疏矩阵),还可以给出精确度很可观的 CQT 逆变换(通过上下采样来调节频段)。
作者提供的 MATLAB 代码可以在下面 👇 的链接中找到(原文中的链接已经失效):
Constant-Q Transform Toolbox:
- A MATLAB reference implementation of a computationally efficient method for computing the constant-Q transform (CQT) of a time-domain signal.
- https://code.soundsoftware.ac.uk/projects/constant-q-toolbox
Python/MATLAB version:
- 我将上述的核心算法代码部分改写为了 Python 版本,也公开如下哈(注意:稀疏矩阵计算的部分并没有改写)
- https://github.com/iphysresearch/CQT_toolbox_python
以下摘自 Repo:
A Python/MATLAB reference implementation of a computationally efficient method for computing the constant-Q transform (CQT) of a time-domain signal.
Note: I just translate the core original MATLAB codes (/MATLAB) to Python version (/CQT.py) with following functions:
Core:
cqticqtgenCQTkernelgetCQTcell2sparsesparse2cellplotCQT
Extra bonus:
bufferupsampleround_half_upnextpow2hann
See the authors’ homepage for more information and MATLAB packaged downloads:
Requirements
- Python 3.6+
- Numpy
- Scipy
- Matplotlib
Demo
Note: It might not be as efficient than the original MATLAB version, partly because the sparse property have yet to be fully utilised in this Python version.
from CQT import *
fname = './demo.dat'
data = np.loadtxt(fname)
t, hp, hc = data[:,0], data[:,1], data[:,2]
fs = 1/(t[1]-t[0])
print('fs =', fs)
bins_per_octave = 24
fmax = 400
fmin = 20
Xcqt = cqt(hp, fmin, fmax, bins_per_octave, fs,)
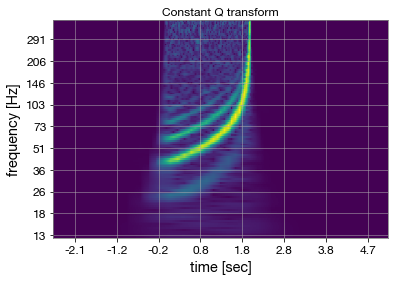
_ = plotCQT(Xcqt, fs, 0.6)
y = icqt(Xcqt)
References
- C. Schörkhuber and A. Klapuri, “Constant-Q transform toolbox for music processing,” in Proceedings of the 7th Sound and Music Computing Conference, Barcelona, Spain, 2010. PDF
- Multipitch Estimation
- 基于音乐识别的频谱转换算法——常数Q变换CQT(转载修改)
- MATLAB codes