S 变换 (Stockwel transform)
S-transform
 Credit by ScienceDirect.com
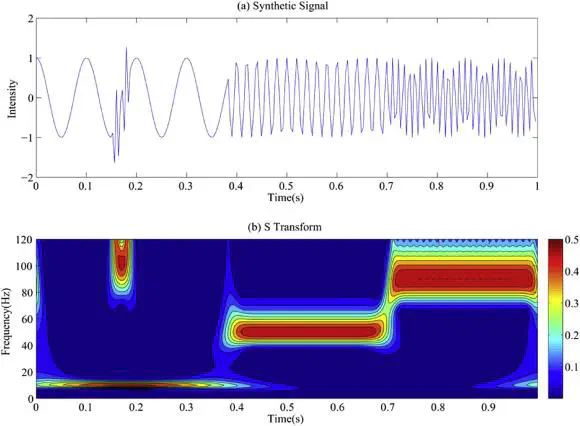
Credit by ScienceDirect.com时频分析示例
REF: https://www.doc88.com/p-0126171299162.html
短时傅里叶变换
短时傅里叶变换是一种单一分辨率的信号分析方法,它的思想是选择一个时频局部化的窗函数,假定分析窗函数g(t)在一个短时间间隔内是平稳(伪平稳)的,移动窗函数,使f(t)g(t)在不同的有限时间宽度 内是平稳信号,从而计算出各个不同时刻的功率谱。短时傅里叶变换使用一个固定的窗函数,窗函数一旦确定了以后,其形状就不再发生改变, 短时傅里叶变换的分新率也就确定了。如果要改变分新率,则需要重新选择窗函数。短时傅里叶变换用来分析分段平稳信号或者近似平稳信号犹可,但是对于非平稳信号,当信号变化剧烈时,要求窗函数有较高的时间分辨率; 而波形变化比较平缓的时刻,主要是低频信号,则要求窗函数有较高的频率分辨率。短时傅里叶变换不能兼顾频率和时间分辨率的需求,由于其窗函数受到Heisenberg不确定准则的限制,时频窗的面积本小于2。这也就从另一个侧面说明了短时傅里叶变换窗函数的时间与频率分辨率不能同时达到最优。
$$F(\omega, t)=\int_{-\infty}^{\infty} e^{-i\omega t’} g\left(t^{\prime}-t\right) f\left(t^{\prime}\right) \mathrm{d} t^{\prime}$$ $$f\left(t^{\prime}\right)=\frac{1}{2 \pi} \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} F(\omega, t) g\left(t-t^{\prime}\right) \mathrm{e}^{-i\omega t^{\prime}} \mathrm{d} \omega \mathrm{d} t$$
Gabor 变换
Gabor变换是Heisenberg不确定准则下的最优的短时傅里叶变换。高斯窗函数是短时傅里叶变换同时追求时间分辨率与频率分辨率时的最优窗函数。具有高斯窗函数的短时傅里叶变换就是Gabor 变换。与短时傅里叶变换一样,Gabor变换也是单一分辨率的。
$$g_{a}(x)=\frac{1}{2 \sqrt{\pi a}} \mathrm{e}^{-\frac{x^{2}}{4 a}}, a>0$$
Wigner-Ville 分布
Wigner-Ville分布,是一种最基本的时频分布,提供了信号清晰的时频关系。它有许多特有的性质,基于这些性质,有着多方面的应用。同时,WVD是时频分布方法的基础,其它的各种分布都是在它的概念上发展起来的。对于单分量线性调频信号,Wigner分布具有很好的时频聚集性,但是这种分布也有它的缺点,例如,正负性,当分析含有多个成分的信号时,分布存在着交叉项,影响了人们对时频分布的正确解释。
小波变换
小波变换使用一个窗函数(小波函数),时频窗面积不变, 但形状可改变。小波函数根据需要调整时间与频率分辨率,具有多分辨分析(Multi-resolution Analysis)的特点,克服了短时傅里叶变换分析非平稳信号单一分辨率的困难。小波变换是一种时间-尺度分析方法,而且在时间、尺度(频率)两域都具有表征信号局部特征的能力,在低频部分具有较高的频率分辨率和较低的时间分辨率,在高频部分具有较高的时间分辨率和较低的频率分辨率,很适合于探测正常信号中夹带的瞬间反常现象并展示其成分。所以,小波变换被称为分析信号的显微镜,但是小波分析不能完全取代傅里叶分析,小波分析是傅里叶分析的发展。
S 变换
S 变换是一种可逆的时频分析方法,它是短时窗傅立叶变换和小波变换的结合。它克服了短时窗傅立叶变换不能调节分析窗口频率的问题,同时引入了小波变换的多分辨率分析,且与傅立叶频谱保持直接的联系,针对地震资料的特点有很好的时频分析能力。Note: $\int_{-\infty}^{+\infty} S(\tau, f) d \tau=H(f)$ , $H(f)$ 为 $h(t)$ 的傅立叶变换。
$$ S(\tau, f)=\int_{-\infty}^{+\infty} h(t) \frac{|f|}{\sqrt{2 \pi}} e^{\frac{(\tau-t)^{2} f^{2}}{2}} e^{-i 2 \pi f t} d t $$ $$ h(t)=\int_{-\infty}^{+\infty}{\int_{-\infty}^{+\infty} S(\tau, f) d \tau} e^{i 2 \pi ft} d f $$
S 变换可以很容易的写成 h(t)的傅立叶变换 H(f)形式:
$$ S(\tau, f)=\int_{-\infty}^{+\infty} H(\alpha+f) e^{-\frac{2 \pi^{2} \alpha^{2}}{f^{2}}} e^{i 2 \pi \alpha \tau} d \alpha $$
S 变换是短时傅立叶变换和小波变换的结合,所以包含了它们的线性特征。对于含噪音的信号,记为: $\operatorname{data}(t)=\operatorname{signal} (t)+\text { noise }(t)$,S 变换给出了以下公式:
$$S T_{\text {data}}=S T_{\text {signal}}+S T_{\text {noise}}$$
Code
- This is a C implementation of the Stockwell Transform.
Book
- Analysis of the Fractional S Transform
- Yu Y., Xu T., Yang P. (2017) Analysis of the Fractional S Transform. In: Shen G., Wu Z., Zhang J. (eds) Advances in Acoustic Emission Technology. Springer Proceedings in Physics, vol 179. Springer, Cham. https://doi.org/10.1007/978-3-319-29052-2_7
概述
Stockwel l R G,Mansinha L P,Lowe R. Localization of the complex spectrum: the S transform. IEEE Transactions on Signal Procesing,1996,44(4):998-1001.
郑成龙,王宝善. S 变换在地震资料处理中的应用及展望. 地球物理学进展 ,2015,30(4):1580-1591.
Zheng Chenglong,Wang Baoshan.Application of S transform in seismic data procesing.Progres in Geo- physics,2015,30(4):1580-1591.
刁瑞,单联瑜,尚新民等. 微地震监测数据时频域去噪方法 [J].物探与化探 ,2015,39(1):112—117.
国内外研究进展
S 逆变换的信号重构过程
Pinnegar (2003) 等提出使用时变滤波函数剔除随机噪声;
Pinnegar C R and Eaton D W.Application of S transform to prestack noise atenuation filtering. Journal of Geophysical Research,2003,108(B9):2422-2443.
高静怀 (2004) 等利用噪声与有效信号间的统计特性差别,在广义 S 变换域识别噪声与有效信号,用 4 个待 定参数的调幅简谐波来代替 S 变换中的基本小波,说明了薄层识别的可行性;
高静怀,陈文超,李幼铭等. 广义 S 变换与薄互层地震响应分析. 地球物理学报,2003,46(4):526-532.
Gao Jinghuai,Chen Wenchao,Li Youming et al. Generalized S transform and seismic response analysis of thin interbeds.Chinese Journal of Geophysics,2003,46(4):526-532.
熊晓军 (2006) 等在其基础上从检测不同信号的到达时间、识别薄层和制作高分辨剖面三个方面研究了广义 S 变换在地震高分辨处理方面的应用;
熊晓军,贺振华,黄德济等. 广义 S 变换在地震高分辨处理中的应用. 勘探地球物理进展,2006,29(6): 415-418.
Xiong Xiaojun,He Zhenhua,Huang Deji et al. Appliation of generalized S transform in seismic high reso- lution procesing. Progres in Exploration Geophysics. 2006,29(6):415-418.
金国平 (2009) 在其基础上结合改进的反褶积方法对地震资料进行了拓频处理;
金国平. 广义 S 变换在地震高分辨率处理中的应用. 石油仪器,2009,23(3):51-53.
Jin Guoping. Application of generalized S transformation to improve seismic data resolution. PI,2009, 23(3):51-53.
刘喜武 (2006) 等提出了基于广义 S 变换的吸收衰减补偿方法;
刘喜武,年静波,刘洪. 基于广义 S 变换的吸收衰减补偿方法. 石油物探,2006,45(1):9-14.
Liu Xiwu,Nian Jingbo,Liu Hong. Generalized S-transform based compensation for stratigraphic absorption of seismic atenuation.GPP,2006,45(1): 9-14.
孙雷鸣 (2011) 等在其基础上进行了改进,利用指数变换的修正规范方差模对补偿后的频谱进行了修正。
孙雷鸣,万欢,陈辉等. 基于广义 S 变换地震高分辨率处理方法的改进及在流花11-1油田的应用. 中国海上油气,2011,23(4):234-237.
Sun Leiming,Wan Huan,Chen Hui et al. An improved method of sesmic high-resolution procesing based on generalized S transform and its application in LH11-1oilfield. China Ofshore Oil and Gas,2011,23(4):234-237.
陈学华 (2006) 等通过引入调节参数 $p$ 和 $\lambda$ 对 S 变换的窗函数进行改造,在信号的时频域中设计两种时频滤波器,滤除特定时频域中的噪声;
陈学华,贺振华,黄德济.基于广义S变换的信号提取与抑噪. 成都理工大学学报 (自然科学版),2006, 33(4):331-335.
Chen Xuehua,He Zhenhua,Huang Deji.Signal extraction and noise suppresion based on generalized S transform.Journal of Chengdu University of Technology (Natural Science Edition),2006,33(4):331-335.
$$ w(t, f)=\frac{\lambda|f|^{p}}{\sqrt{2 \pi}} \mathrm{e}^{\frac{-\lambda^{2} f^{2p} t^2}{2}} $$
Schimmel (2005) 等指出基于反 S 变换时频滤波方法存在的问题,并提出一种新的反 S 变换方法,用于时频滤波;
Schimmel M and Galart J.The inverse S transform in filters with time-frequency localization.IEEE Transactions on Signal Procesing,2005,53(11):4417-4422.
赵淑红 (2007) 等证明了基于 S 变换的时频滤波去噪方法,可以克服传统方法中滤波因子不能随时间、频率而变化的缺陷;
赵淑红,朱光明. S 变换时频滤波去噪方法. 石油地球物理勘探,2007,42(4):402-406.
Zhao Shuhong,Zhu Guangming. S-transform time-frequency filter de-noising method.OGP,2007,42(4): 402-406.
$$ H(n, k)=\begin{cases} 1 & k \in\left[f_{i}(n)-B(n) / 2, f_{i}(n)+B(n) / 2\right] \\ 0 & \text { 其他 } \end{cases}. $$
张晓峰 (2010) 提出对信号进行广义 S 变换后,对获得的含噪时频剖面选取适当阈值函数压制噪声,从而提取有效信号重构去噪后的地震记录。
张晓峰. 基于广义 S 变换的地震资料信噪分离方法. 物化探计算技术,2010,32(5):480-483.
Zhang Xiaofeng. Signal segmentation of seismic data based on generalized S transform. Computing Techniques for Geophysical and Geochemical Exploration,2010,32(5):480-483.
基于 S 变换的低信噪比阈值滤波
金智尹 (2015) 等在 S 变换的基础上,根据信号时频分布构造三种高斯邻域局部阈值滤波方法用于高精度滤波去噪;
金智尹,柏强. 基于广义S变换的高斯领域时频滤波方法. 电子测量与仪器学报,2015,29(1):125-131.
Jin Zhiyin,Bai Qiang. Time-frequency filtering in Gausian domain based on generalized S-transform. Journal of Electronics & Measurements,2015,29(1): 125-131.
刘永春 (2011) 等比较了基于广义 S 变换的三种时频率滤波方法对声波反射信号的去噪效果;
刘永春,童敏明,陈琳等. 基于广义S变换的声发射信号去噪研究. 计算机应用研究,2011,28(12):4535-4536.
Liu Yongchun,Tong Minming,Chen Lin et al. Research on de-noising of acoustic emision signals based on generalized S transform. Application Research of Computers,2011,28(12):4535-4536.
李雪英 (2011) 等对基于广义 S 变换和经验模态分解的高频噪声压制方法在去噪原理、去噪效果、计算效率、保真度等方面进行了对比分析。
李雪英,孙丹,侯相辉等. 基于广义 S 变换、经验模态分解叠前去噪方法的比较. 地球物理学进展,2011, 26(6):2039-2045.
Li Xueying,Sun Dan,Hou Xianghui et al. Comparison of pre-stack de-noising method based on generalized S-transform and empirical mode decomposition.Progres in Geophysics,2011,26(6):2039-2045.
张岩 (2017) 等依据图像块分组稀疏表示思想,利用邻近地震数据块之间多个地震记录道的相似性,提出基于多道相似组稀疏表示的地震数据随机噪声压制方法;
张岩,任伟建,唐国维. 利用多道相似组稀疏表示方法压制随机噪声. 石油地球物理勘探,2017 ,52 (3 ):442-450.
Zhang Yan,Ren Weijian,Tang Guowei. Random noise suppresion based on sparse representation of multitrace similarity group.OGP,2017,52(3):442-450.
张华 (2017) 等提出使用二维曲波变换对含噪三维地震数据的时间切片进行多尺度、多方向分解,在曲波域采用阈值法压制随机噪声;
张华,陈小宏,李红星等. 曲波变换三维地震数据去噪技术. 石油地球物理勘探,2017,52(2):226-232.
Zhang Hua,Chen Xiaohong,Li Hongxing et al. 3D seismic data de-noising approach based on Curvelet transform .OGP,2017,52(2 ):226-232.
张恒磊 (2017) 等基于反射波各向异性、随机噪声各向同性特征,通过构造各向异性函数进行加权叠加的数据保真处理,实现地震数据保真去噪;
张恒磊,胡哲,胡祥云等. 基于反射波各向异性特征的保真去噪方法. 石油地球物理勘探,2017 ,52 (2 ):233-241.
Zhang Henglei,Hu Zhe,Hu Xianyun et al. Seismic fidelity denoising method with reflection anisotropy. OGP,2017,52(2):233-241.
宋维琪 (2015) 等针对地面微地震检测资料中噪声特点研究地面微地震资料 τ-p 变换去噪方法;
宋维琪,刘太伟. 地面微地震资料 τ-p 变换噪声压制. 石油地球物理勘探,2015,50(1):48-53.
Song Weiqi,Liu Taiwei. Noise suppresion by τ-p transform of surface microseismic data.OGP,2015, 50(1):48-53
赵军龙 (2016) 等比较分析了小波去噪算法与希尔伯特—黄变换滤波算法在不同信噪比情况下对常规测井曲线的滤波效果的差异;
赵军龙,刘建建. 常规测井曲线的小波和希尔伯特—黄变换滤波效果分析. 石油地球物理勘探,2016,51(4):801-808.
Zhao Junlong,Liu Jianjian. Analysis of wavelet and Hilbert-Huang transform filtering of conventional wel logging curve.OGP,2016,51(4):801-808 .
调整窗函数获得多种非线性变化特征
Mansinha (1997) 等用 (f/r) 代替 f,得到调谐的高斯函数,允许使用者自定 S 变换在时频面上时间和频率的分辨率;
Mansinha L,Stockwell R G,Lowe R P,et al. Local S—spectrum analysis of 1一D and 2一D data [J]. Physics of the Earth and Planetary Interiors,1997,103(3):329—336.
Pinnegar (2003) 等提出用非对称的双曲窗代替高斯窗,用于地震波的 P 波首波时间的判定;
Pinnegar C R,Mansinha L. Time-local spectral analysis for non-stationary time series: the S-transform for noisy signals [J]. Fluctuation and Noise Leters,2003,3(03):L357-L364.
Wang (2015) 等基于信号的广义S变换时频域数据,根据有效信号与噪声的能量差异提出一种新的数据自适应滤波算法,用于抑制有效信号在时频域中的随机噪声;
Wang D,Wang J,Liu Y et al. An adaptive time-frequency filtering algorithm for multi-component LFM signals based on generalized S-transform.IEEE International Conference on Automation and Computing,2015,1-6.
Duan Li (2013) 等提出一种修正的 S 变换新方法,对高斯窗函数进行改进,利用一个线性频率方程代替高斯窗的频率,调节时窗宽度随频率呈反比变化的速度,提高了 S 变换在具体应用中的实用性和灵活性;
Li D,Castagna J. Modified S-transform in time-frequency analysis of seismic data [C] // 2013 SEG Annual Meeting. Society of Exploration Geophysicists,2013.
张先武 (2013) 等在 S 变换的时窗函数中引入调节参数的同时加入低通滤波函数,推导出一种新的广义 S 变换算法,并使用该算法对探地雷达数据进行层位识别,取得了较好效果;
张先武,高云泽,方广有. 带有低通滤波的广义 S 变换在探地雷达层位识别中的应用. 地球物理学报,2013 , 56(1):309-316.
Zhang Xianwu,Gao Yunze,Fang Guangyou. Application of generalized S-transform with low-pass filter in ground penetrating radar layer recognition. Chinese Journal of Geophysics,2013,56(1):309-316.
黄捍东 (2014) 等在广义 S 变换 (陈学华 et al. 的窗口函数) 实现时引入一系列函数库和快速傅里叶变换,使运算简洁高效,并通过选取合适参数组合对时频谱进行能量重新分配重构,获得高分辨率的地震信号。
黄捍东,冯娜. 广义 S 变换地震高分辨率处理方法研究. 石油地球物理勘探,2014,49(1):82-88.
Hunag Handong,Feng Na. High-resolution seismic procesing method based on generalized S transform. OGP,2014,49(1):82-88.
$$ w(t, f)=\frac{\lambda|f|^{p}}{\sqrt{2 \pi}} \mathrm{e}^{\frac{-\lambda^{2} f^{2p} t^2}{2}} $$
$$ \text{GST}_{x}(\tau, f)=\Big(x(\tau) {e}^{-i 2 \pi f z}\Big) \star\Big(\frac{\lambda|f|^{p}}{\sqrt{2 \pi}} {e}^{\frac{-\lambda^{2} f^{2 p} x^{2}}{2}}\Big) $$ $$ \text{GST}_{x}(i, j)=[e_{j}(i) \cdot x(i \Delta t)] * w_{j}(i) $$
阮清青 (2017) 等人利用频率相关的一阶线性方程来代替归一化高斯窗口函数中的频率。
阮清青,张会星,王昊,李凯瑞. 修正 S 变换与常规时频分析方法的对比. 中国煤炭地质, 1674—1803(2017)04-0066-07
Ruan Qingqing,Zhang Huixing,Wang Hao and Li Kairui. Comparison of Modified S-transform (MST) and Traditional Time-Frequency Analysis Methods. 1674—1803(2017)04-0066-07
$$ w(t, f)=\frac{|mf+n|}{\sqrt{2 \pi}} {e}^{\frac{- |mf+n|^2 t^2}{2}} $$
曹鹏涛 (2018) 等在 Pinnegar 方法基础上,采用非对称双曲线窗函数,改进时频滤波函数,联合高斯平滑滤波函数提出一种数据 自适应的高频噪声压制方法;
曹鹏涛,张敏,李振春. 基于广义 S 变换及高斯平滑的自适应滤波去噪方法. 石油地球物理勘探,2018,53(6): 1128-1136,1187.